Чистые и смешенные ансамбли. Матрица плотности

Квантовая теория

Семестр I

Лекция VIII

Чистые и смешенные ансамбли. Матрица плотности.

Как описывать системы, которые являются случайной смесью отдельных квантовых систем?

Чистые и смешанные ансамбли

Что ансамблю квантовых состояний?

I. Статистический ансамбль квантовых систем

Ансамбль – это такая совокупность одинаковых экземпляров одной и той же физической системы, в которой реализуются все возможные микросостояния этой системы, отличающиеся значениями случайных внутренних параметров при одинаковых внешних условиях существования системы.

I. Статистический ансамбль квантовых систем

Пример – термодинамический ансамбль классической механики. В элементах такого ансамбля реализуются все возможные микросостояния системы с различными положениями молекул в пространстве и значениями скоростей.

I. Статистический ансамбль квантовых систем

Пусть {ΨE} – совокупность допустимых состояний квантовой системы определенного типа, которые являются решением уравнения Шредингера:

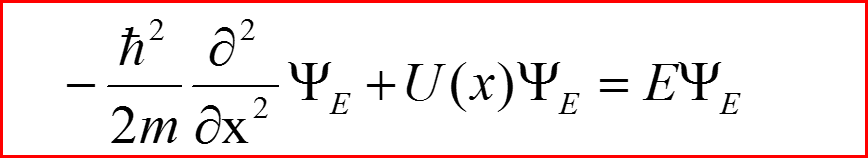
I. Статистический ансамбль квантовых систем

Чистым ансамблем называется совокупность квантовых систем, находящихся в одном и том же квантовом состоянии, т.е описывающихся одной и той же волновой функцией Ψ , в частности ΨE.

I. Статистический ансамбль квантовых систем

Смешанным ансамблем называется совокупность квантовых систем, находящихся в различных квантовых состояниях, т.е описывающихся разными волновыми функциями из данной допустимой совокупности {Ψ} , в частности {ΨE} для всевозможных допустимых значений E.

II. Смешанный ансамбль квантовых систем

Смешанный ансамбль характеризуется набором волновых функций {ΨE} и вероятностями P{E} обнаружить в ансамбле систему с заданной волновой функцией ΨE из данного набора.

Смешанный ансамбль в дальнейшем будем обозначать через {ΨE, P{E}} .

II. Смешанный ансамбль квантовых систем

Для смешанного ансамбля {ΨE, P{E}} вероятность обнаружить частицу в точке с координатами x в момент времени t определяется выражением:

II. Смешанный ансамбль квантовых систем

Среднее значение динамических переменных в чистом ансамбле

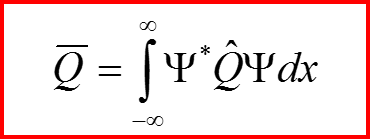
Среднее значение динамических переменных в смешанном ансамбле

III. Матрица (оператор) плотности

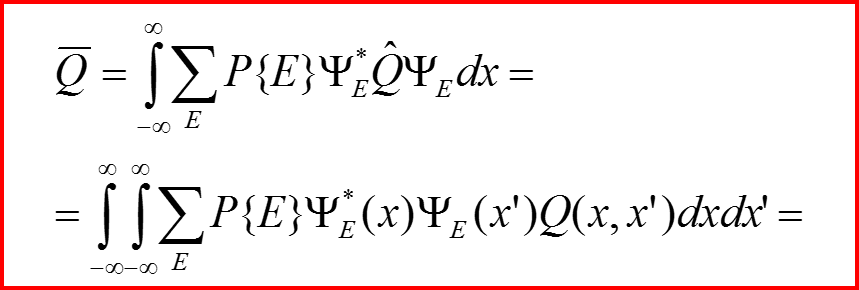
Матрица плотности:

III. Матрица (оператор) плотности

Оператор плотности в общем случае:

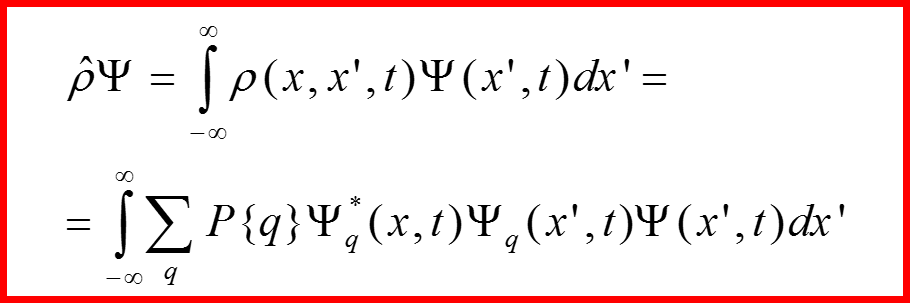
III. Матрица (оператор) плотности

Уравнение для оператора плотности:

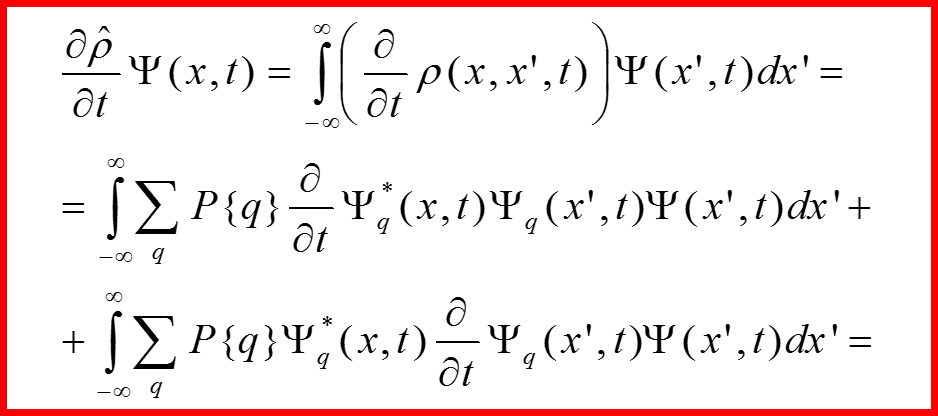
III. Матрица (оператор) плотности

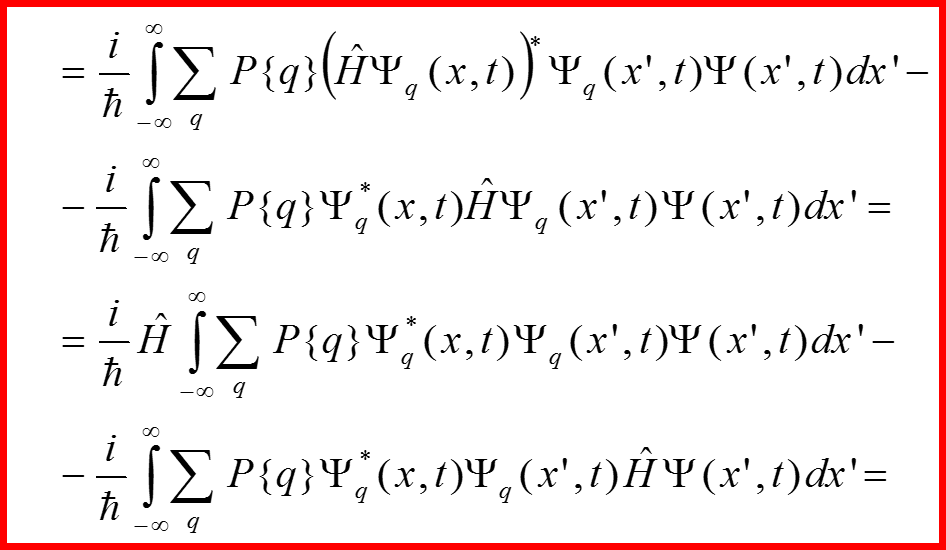
III. Матрица (оператор) плотности

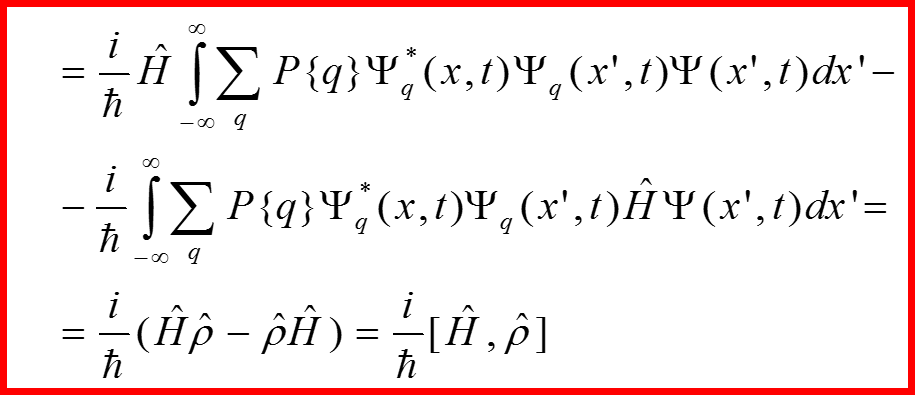
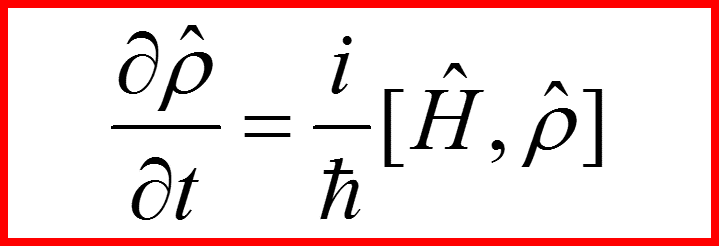
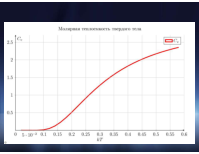
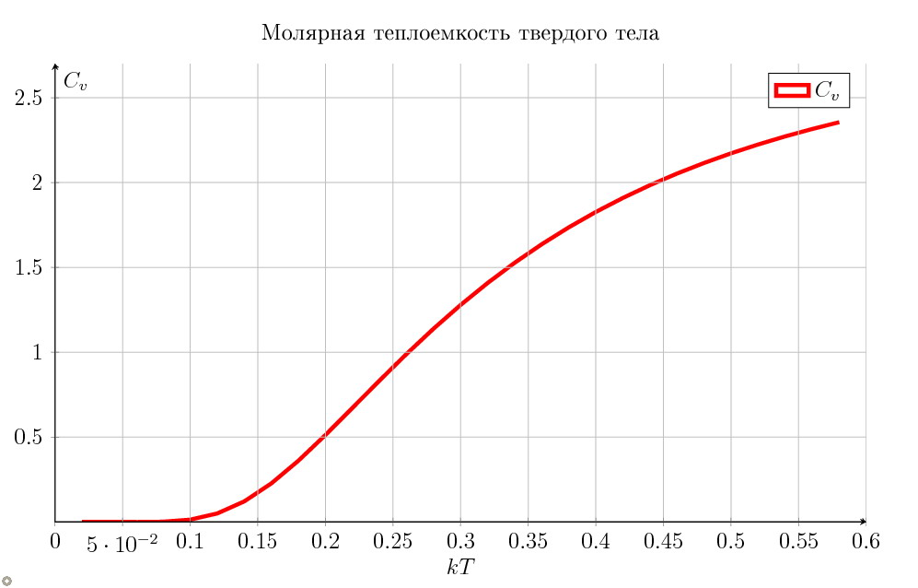
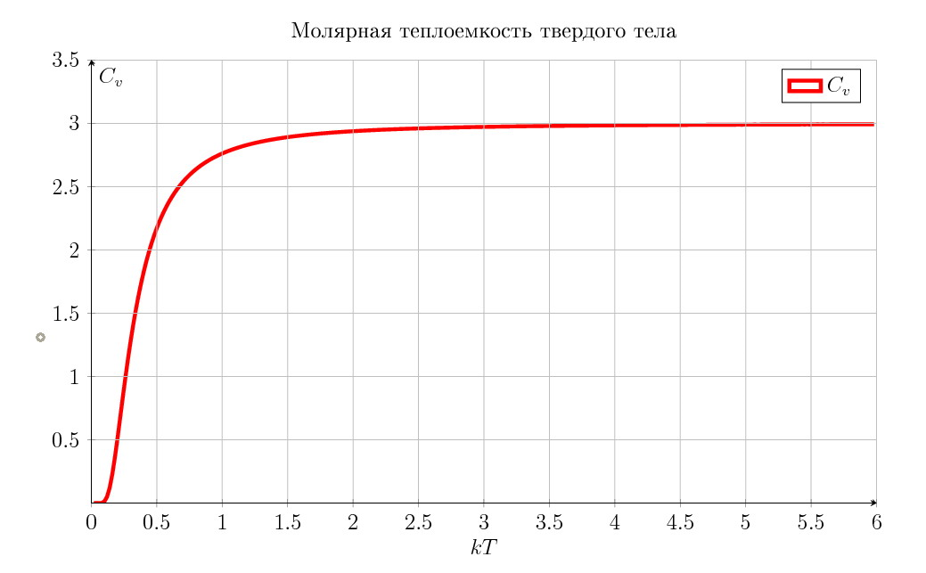
Пример: Теплоемкость твердых тел (теория Эйнштейна)

Классическая теория-закон Дюлонга-Пти: Молярная теплоемкость твердых тел равна:

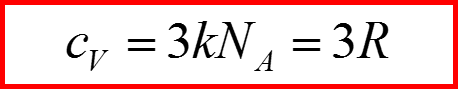
Na-число Авогадро, k- постоянная Больцмана, R=kNa

Вычисление теплоемкости. Классический случай.

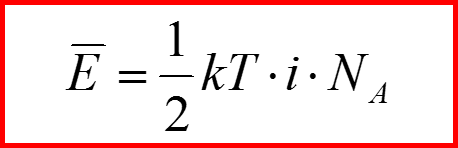
На каждую степень свободы приходится 1/2kT, i=6 для каждого гармонического осциллятора

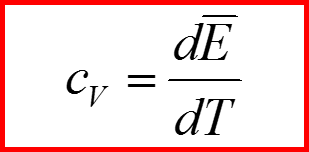
Вычисление теплоемкости. Квантовый случай.

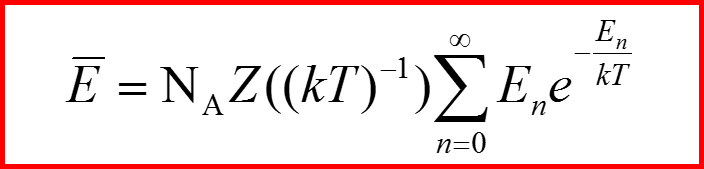
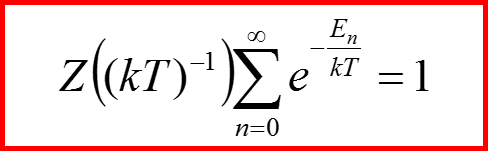
Условие нормировки →

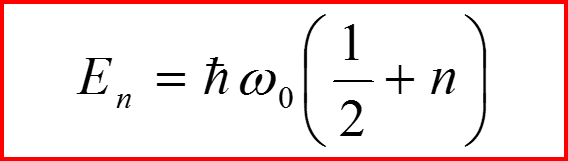
Вычисление теплоемкости. Квантовый случай.

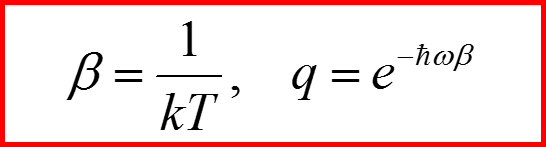
Обозначим →

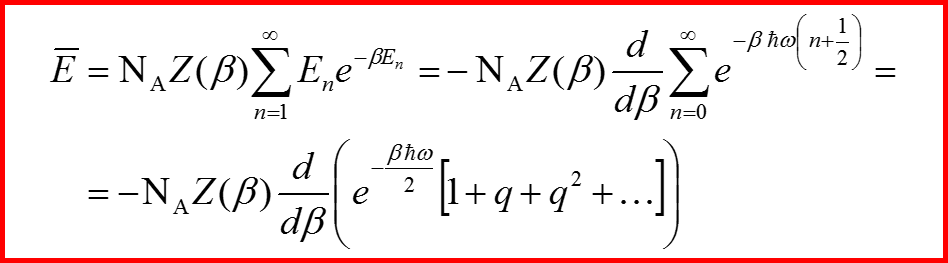
Вычисление теплоемкости. Квантовый случай.

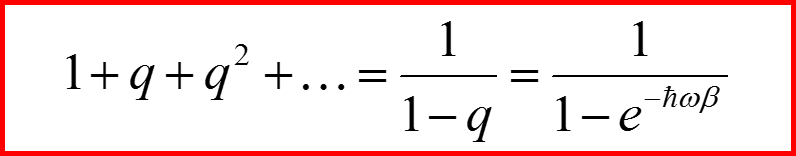
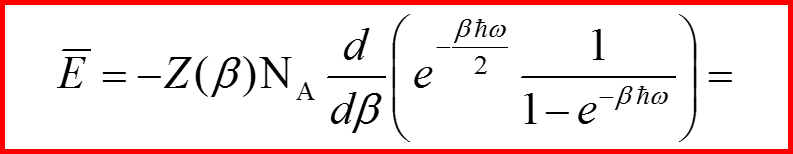
Вычисление теплоемкости. Квантовый случай.

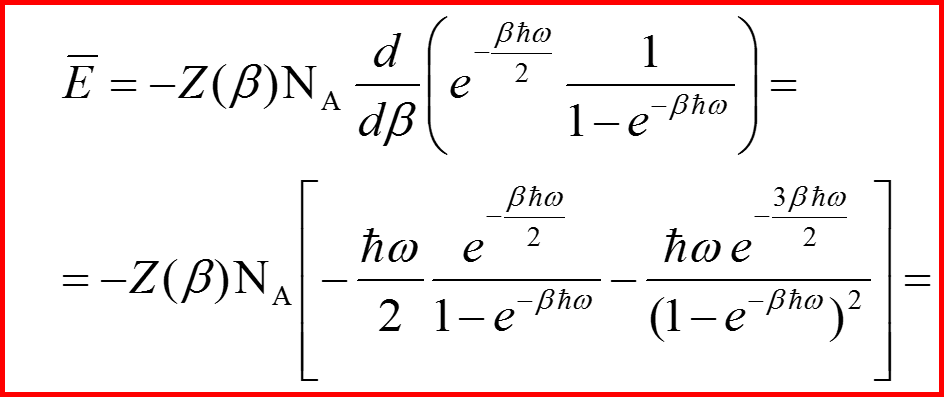
Вычисление теплоемкости. Квантовый случай.

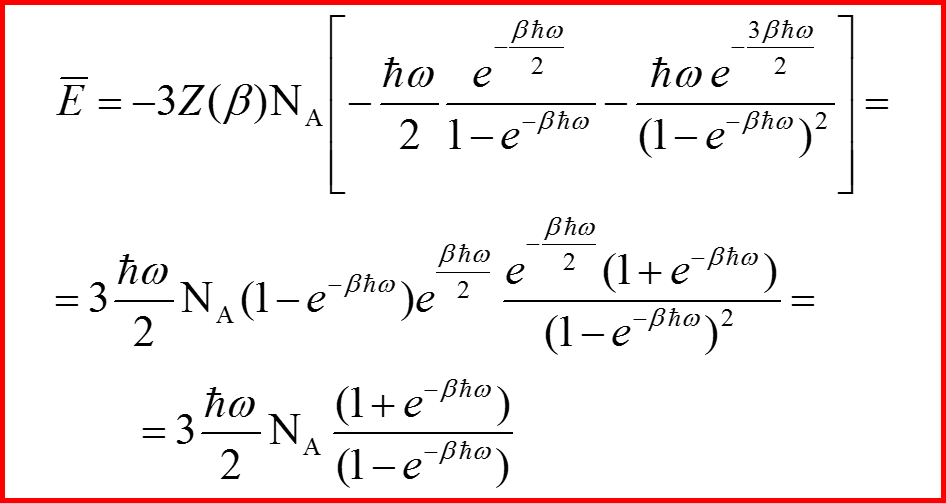
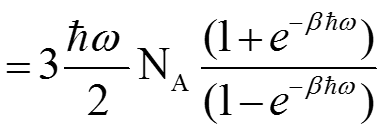
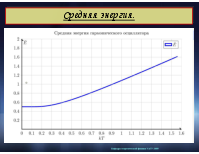
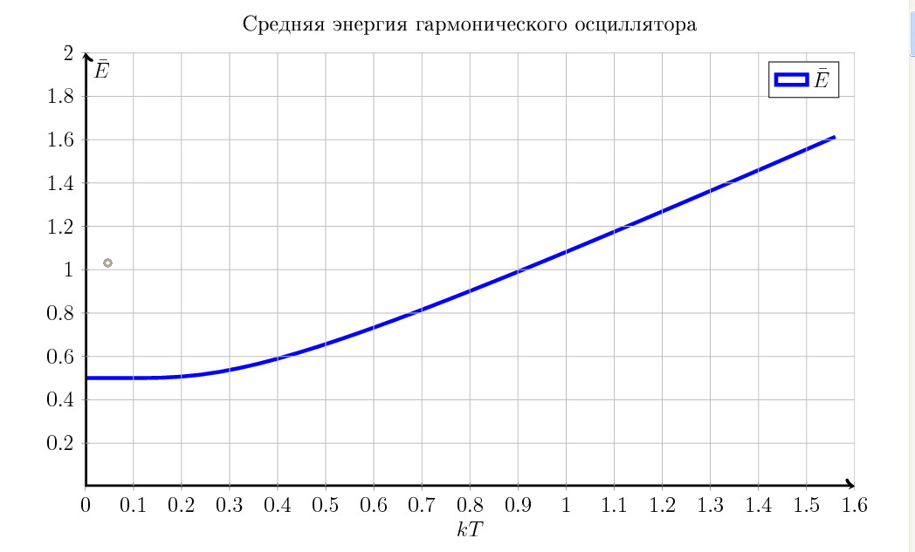
Средняя энергия.

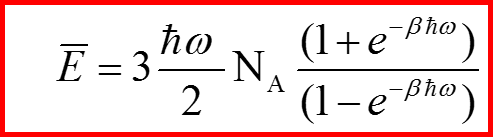
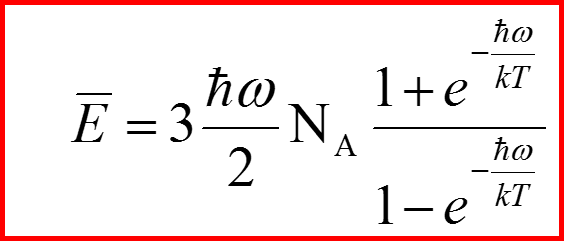
Средняя энергия.

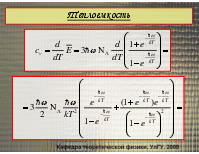
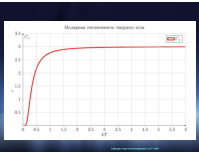
Теплоемкость

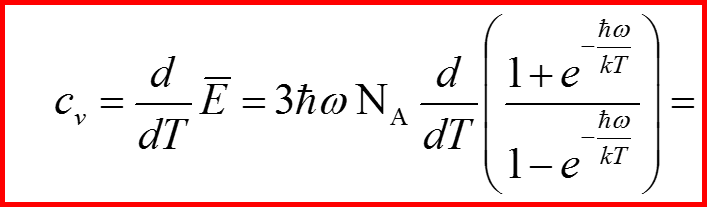
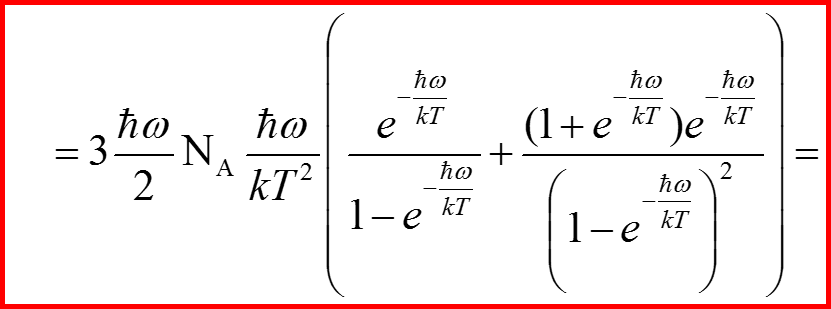
Теплоемкость

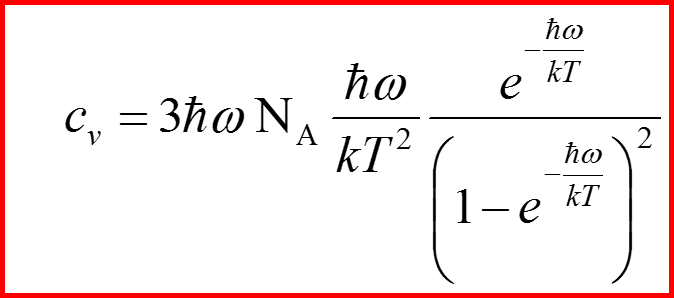
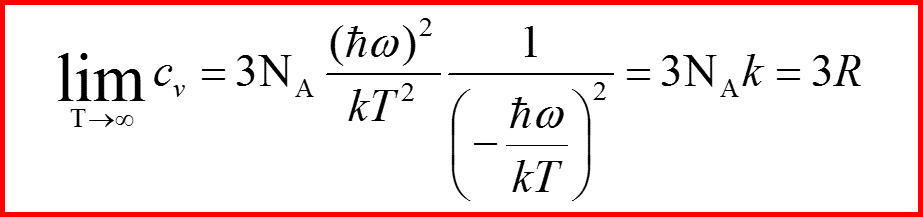
Следующая лекция

Методы решения квантовых задач