Сравнение графиков интерполяционных полиномов в форме Ньютона Pn (x), страница 3

%                   x     - массив точек

%                   n     – степень полинома

%

%Выходные значения: x_massiv – массив точек разбиения

function rr_massiv = RRFn(y_fun, x, n)

    rr_matrix = zeros(n+1, n+1);

    for t = 1: 1: n + 1

        rr_matrix(t, 1) = y_fun(t);

    end

    for u = 1: 1: n

        for t = 1: 1: n

            if t + u <= n + 1

                rr_matrix(t, u + 1) = (rr_matrix(t + 1, u) - rr_matrix(t, u))/(x(t + u) - x(t));

            end

        end

    end

    for t = 1: 1: n + 1

        rr_massiv(t) = rr_matrix(1, t);

    end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

y_funFn.m

%Входные значения:  x – массив точек

%       

%Выходные значения: y_fun – массив значений в точках

function y_fun = y_funFn(x)

    for n = 1 : 1 : numel(x)

        if x(n) > 0

            y_fun(n) = x(n)^2;

        else

            y_fun(n) = 0;

        end

    end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

y_polFn.m

%Входные значения:  n    – степень полинома

%                   razb – выбор разбиения

%

%Выходные значения: y_pol – массив значений интерполяционного полинома

function y_pol = y_polFn(n, razb)

    x_razb = razbFn(n, razb);

    y_fun = y_funFn(x_razb);

    rr_massiv = RRFn(y_fun, x_razb, n);

    y_pol = polFn(rr_massiv, x_razb, n);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

5.  Результат.

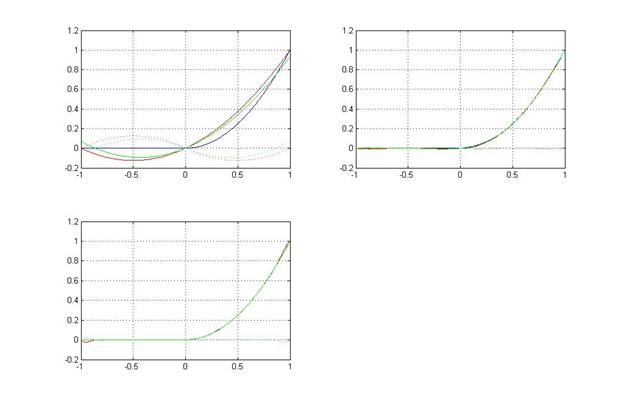
6.  Выводы.

Были построены графики интерполяционных полиномов при равномерном выборе узлов и при выборе узлов по Чебышеву 2-ого, 6-ого и 14-ого порядков. При равномерном выборе узлов на концах заданного интервала при достаточно больших n происходит сильное увеличение погрешности. При выборе узлов по Чебышеву функция апроксимируется более точно.