Устойчивоcть и управляемость электрических систем с автоматическим регулированием: Методические указания к практическим занятиям по дисциплине «Переходные процессы в энергетических системах», страница 3

Нас интересует , то есть изменение ЭДС от интересующего нас параметра. Для определения этого изменения необходимо составить систему уравнений, отражающих переходной процесс в машине и АРВ, и решать их совместно. Этому препятствует нелинейность элементов систем и разброс постоянных времени их (от сотых долей секунды до нескольких секунд). Решение традиционными методами требует уменьшения шага расчета  до  ~0,1 от минимальной постоянной времени элемента, то есть проведения расчета в  шагов. Это, в свою очередь, увеличивает суммарную погрешность расчета настолько, что сам расчет теряет смысл.

Чтобы не понижать точность и не увеличивать объем вычислений можно разделить задачу на две:

1. определение                                           

2. учет                                                               причем связь  нашей системы описывается линейным уравнением

                                    

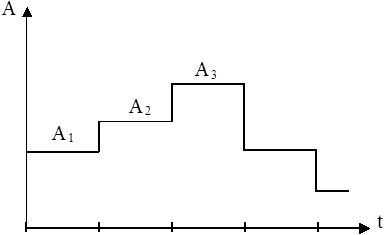
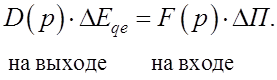
Обозначив , будем считать  постоянной на каждом расчетном интервале. Значения этой функции могут быть найдены численно через производные ; ; ; .

Воспользуемся численным методом дифференцирования по трем значениям функции равностоящих точек.

          

                      

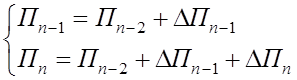
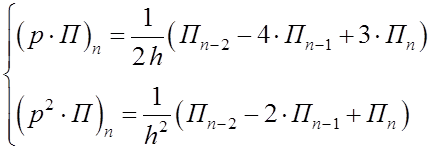
Подстановкой в получим

                      

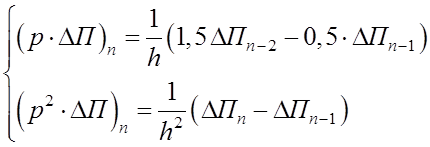
Теперь задача сводится к решению линейного дифференциального уравнения

Вводя переходную функцию  так, чтобы

,                                                          получаем

         

                        

Этот метод базируется на теореме свертки в операторном исчислении.

Пример 1. Определение ЭДС синхронной машины с АРВ пропорционального действия.

Если не учитывать запаздывание в цепи АРВ, то

              

Заменив действительное изменение ступенчатым, получим

                                                     

Приняв , получим

                                                       

        

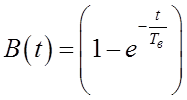
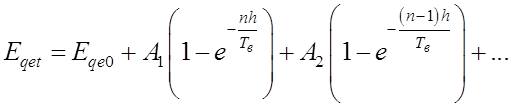
Пример 2. Определение изменения ЭДС при воздействии АРВ сильного действия.

                                                                  

              .

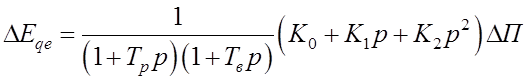Тогда                                           

             

Переходная функция

                                  

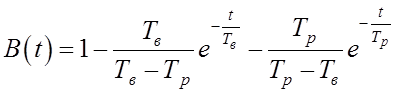
Примечание: точность расчета может быть повышена в этом случае или изменением коэффициентов усиления, компенсирующим неполный учет нелинейности процесса, или изменением д.у. переходного процесса.

Отличие воздействия АРВ сильного действия можно показать на простейшем примере. Предположим, что на АРВ выставлены 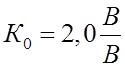;  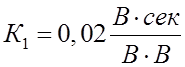(значения условные).

В рабочем режиме напряжение снизилось на 500 В за 1,0 сек.

АРВ пропорционального действия отреагирует добавкой

.

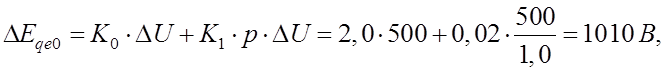
то есть влияние части сильного регулирования при таком медленном изменении режима весьма мало.

При коротком замыкании напряжение снижается на 500 В за 0,01 сек. Реакция АРВ пропорционального действия, зависящая только от величины отклонения, остается прежней. Реакция АРВ сильного действия

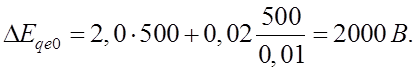
Примем =1,0 сек  и =0,2 сек (условно).

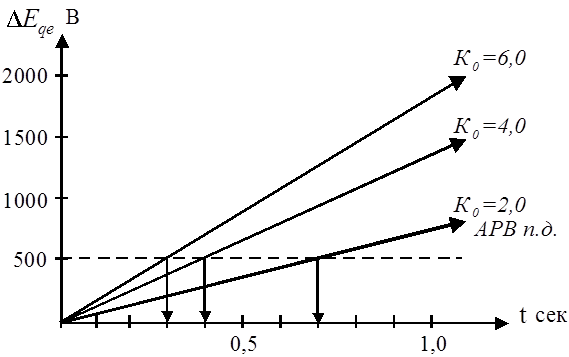
Приведенные на рис. 6 кривые показывают, что даже существенное увеличение коэффициента усиления по отношению  не дает возможности быстрого увеличения возбуждения, но это достигается наличием составляющей по производной отклонения .

а) Реакция АРВ 1,0 при медленном изменении напряжения б) Реакция АРВ при быстром изменении напряжения

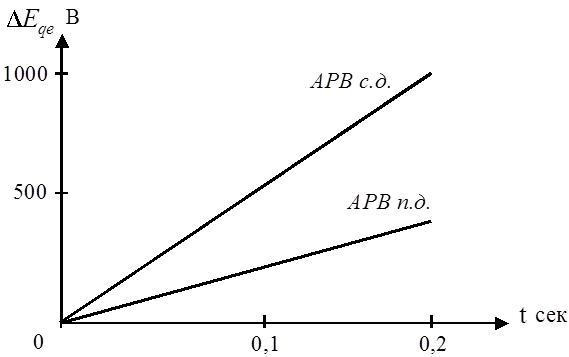Рис. 6

Необходимость определения коэффициентов регулирования заставляет нас прибегать к частным критериям и методам, одним из которых является метод D-разбиения. Подробное изложение и обоснование этого метода будет приведено в другой работе, здесь мы ограничиваемся лишь изложением необходимого минимума. В характеристическом уравнении выделяется часть, отражающая регулирование и все регулируемые параметры принимаются постоянными, кроме двух.

Это позволяет построить границу области устойчивости в плоскости этих двух параметров. Постепенное ужесточение условий (увеличение других параметров  шаг за шагом) позволяет исследовать изменение области устойчивости (сужение области до исчезновения ее). Расчет повторяется при замене одного из регулируемых параметров на последующий с фиксацией значения предыдущего (то есть исследование, например  от , затем  от  и т.д.). Задача очень трудоемка, даже при использовании ЭВМ, но область решения находима.

Литература

1.  Жданов П.С. Устойчивость электрических систем. - М.: Высшая школа, 1990.

2.  Веников В.А. Электромеханические переходные процессы. – М.: Высшая школа, 1985.

3.  Электрические системы: математические задачи электроэнергетики. Под ред. В.А. Веникова. – М.: Высшая школа, 1981.

4.  Методика расчетов устойчивости автоматизированных электрических систем. Под ред. В.А. Веникова. – М.: Высшая школа, 1967.

5.  Веников В.А., Анисимова М.Д. и др. Электроэнергетические системы в примерах и иллюстрациях. – М.: Энергоатомиздат, 1983.