Устойчивоcть и управляемость электрических систем с автоматическим регулированием: Методические указания к практическим занятиям по дисциплине «Переходные процессы в энергетических системах», страница 2

- передаточная функция, связывающая сигнал (возмущение) на входе системы с ее реакцией на выходе.

После приведения к общему знаменателю мы получаем выражение

                           

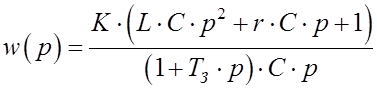
На изменение входной величины система может реагировать по разному.

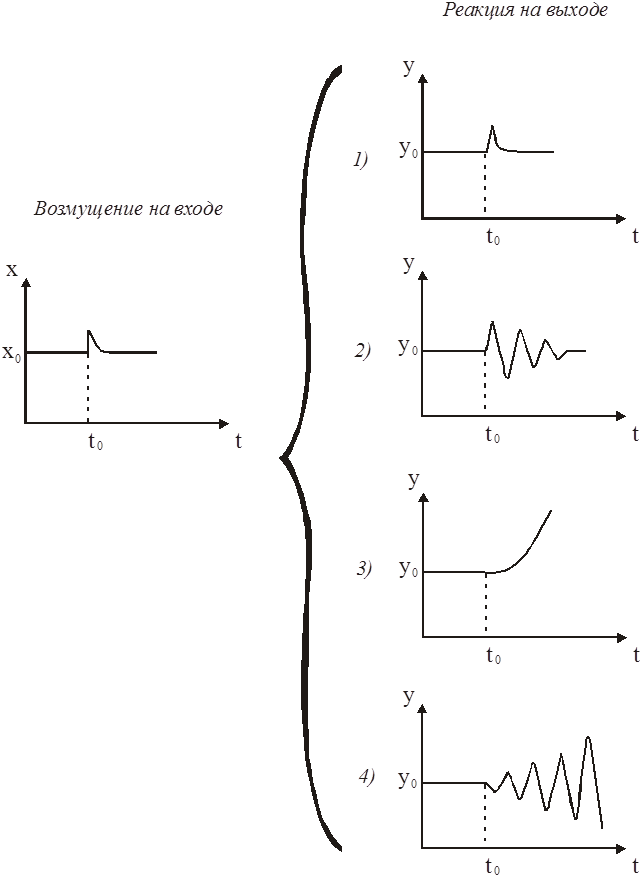
Рис. 4.

В 1 и 2 случаях мы считаем, что система устойчива, в 3 и 4 – неустойчива, причем нарушение устойчивости может носить как апериодический (3), так и периодический характер (4).

В общем случае выражение может быть записано

                              где  - выражения, включающие параметры системы и режима и коэффициенты регулирования АСУ.

Согласно И. Ньютону выражение может быть представлено в виде

,                        где  - корни характеристического уравнения

.                               

Каждый сомножитель в изображении  соответствует выражению  в оригинале, если  - вещественный корень, или , если  - пара корней вида .

В случае хотя бы одного > 0, реакция системы на возмущение будет иметь вид рис 4.3 для вещественного корня и рис 4.4 для пары корней с мнимой частью, т.е. система будет неустойчива, даже если все остальные корни характеристического управления будут иметь .

Получить характеристическое управление удается лишь для сравнительно простого случая. Обычно мы получаем систему уравнений, например, для случая простейшей системы автоматического регулирования возбуждения пропорционального регулирования.

   

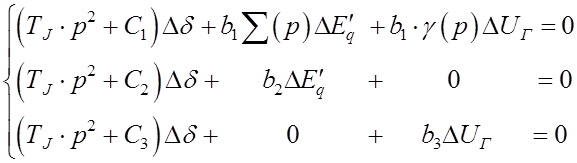
где ,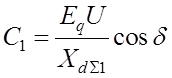   

             

       

       

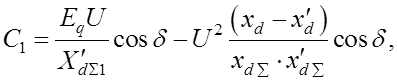
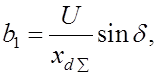
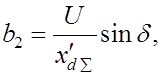
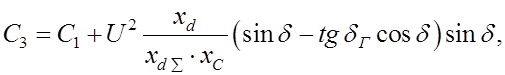
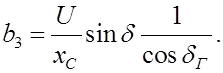
Анализ устойчивости такой системы проводим, используя алгебраические критерии Гурвица, Рауса по знакам и соотношениям коэффициентов и определителей более низкого порядка, составленных по определенным правилам ( и т.д.).

Пример. Исследование устойчивости системы по критерию Гурвица

Уравнения, которые описывают поведение системы:

При малых возмущениях  можно считать неизменными. Они меняются при изменении режима.

Перепишем уравнения относительно

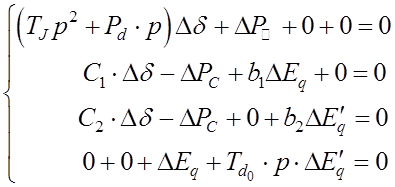
Получаем определитель

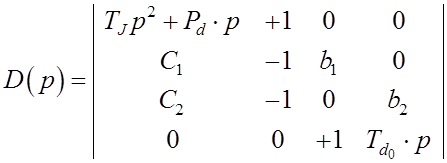
Раскрываем определитель как характеристичеcкое уравнение

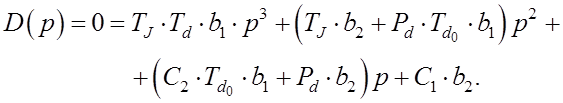
Разделив на  и заменив 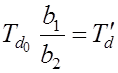, получим

характеристическое уравнение 3-го порядка.

По критерию Гурвица для отсутствия положительных корней необходимо, чтобы все коэффициенты  и так называемый определитель Гурвица были положительны.

Определитель Гурвица

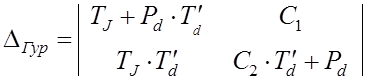
Когда же могут появиться или положительные корни или комплексные корни с положительными вещественными частями?

1.Свободный член

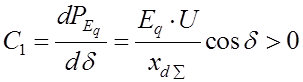 при , то есть система может быть устойчива только при . При  - критический режим и медленное без качаний (апериодическое) нарушение устойчивости (сползание).

2. Коэффициент при

 может стать , если .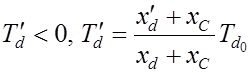

Это возможно при  (емкость), причем . При этом возникает колебательное нарушение устойчивости (самовозбуждение). Оно может практически возникать и при  при .

3. Коэффициенты при  и

При          

при             

могут стать , если , но должно быть  

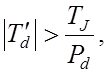
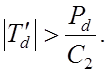
4. Требование  приводит к условию

Легко показать, что это условие обращается в 0 только при  и  (отсутствие демпфирования).

То есть самораскачивание возможно в системе с малым  и режимом, близким к режиму холостого хода.

Проведенное исследование позволило выявить режимные условия нарушения устойчивости. Исследование процессов в системе при регулировании параметров представляет отдельную и наиболее сложную задачу. Как правило в этом случае не удается получить решение в виде простого соотношения, и в силу сложности системы, разномасштабности параметров и коэффициентов регулирования, а также нелинейности элементов.

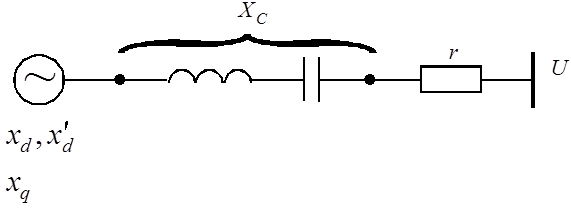a)

б)

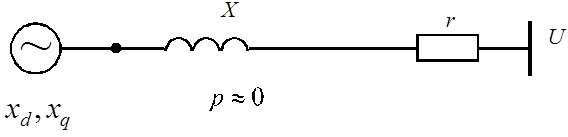в)

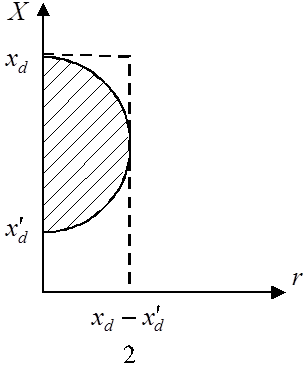
Рис. 5. Условия появления самовозбуждения и самораскачивания:

а) схема, характерная для условий возникновения самовозбуждения;

б) схема, характерная для условий возникновения самораскачивания;

в) область самовозбуждения в координатах

3. Управляемость систем с автоматическим регулированием возбуждения

Если устойчивость системы с автоматическим регулированием рассматривается чрезвычайно подробно, в особенности части определения границ устойчивости, то управляемость системы в пределах границ устойчивости не рассматривается в общедоступной литературе. Наиболее просто этот вопрос решается в предположении , однако эта ЭДС изменяется как вследствие переходных процессов в машине, так и в результате воздействия АРВ.