Полный анализ цепи заключается в нахождении токов, напряжений и их фаз на всех участках цепи.
Дифференциальное уравнение, описывающее колебания тока и напряжения в цепи с активным и индуктивным сопротивлением имеет вид
![]() (2)
(2)
где
![]() - полное активное сопротивление
цепи, включающее активное сопротивление катушки
- полное активное сопротивление
цепи, включающее активное сопротивление катушки ![]() и
ограничивающее ток сопротивление
и
ограничивающее ток сопротивление ![]() :
: ![]() .
.
Для его решения могут быть использованы различные методы: алгебраический, метод векторных диаграмм и др.
Алгебраический метод для установившихся вынужденных колебаний в цепи заключается в том, что мы ищем решение уравнения (2) в виде
![]() , (3)
, (3)
где
![]() - угол сдвига между током
- угол сдвига между током ![]() и приложенным напряжением
и приложенным напряжением ![]() . Подставляя (3) в уравнение (2) и
приравнивая множители при членах
с
. Подставляя (3) в уравнение (2) и
приравнивая множители при членах
с ![]() и
и
![]() , получим
, получим
![]() , (4)
, (4)
![]() , (5)
, (5)
откуда
![]() , (6)
, (6)
![]() , (7)
, (7)
где
роль индуктивного сопротивления играет величина ![]() .
.
Рассмотрим метод векторных диаграмм для цепи переменного синусоидального тока с активным и индуктивным сопротивлением.
Этот метод обладает большой наглядностью. Напряжение ![]() , приложенное к цепи, одновременно существует на
активном
, приложенное к цепи, одновременно существует на
активном ![]() и индуктивном
и индуктивном ![]() сопротивлениях
сопротивлениях
![]() и
и ![]() . (8)
. (8)
Для построения результирующего напряжения ![]() по составляющим
по составляющим ![]() и
и
![]() , необходимо векторно сложить
, необходимо векторно сложить ![]() и
и ![]() на
векторной диаграмме. Подчеркнем что
на
векторной диаграмме. Подчеркнем что ![]() и
и ![]() характеризуются величиной и фазой
(углом) и поэтому могут быть представлены на плоскости в виде векторов. Для
удобства будем строить диаграммы, используя действующие значения величин
характеризуются величиной и фазой
(углом) и поэтому могут быть представлены на плоскости в виде векторов. Для
удобства будем строить диаграммы, используя действующие значения величин ![]() и
и ![]() ,
которые в
,
которые в ![]() раз меньше их амплитуд.
раз меньше их амплитуд.
|
|
Действующее значение силы тока ![]() одно
и то же в сопротивлениях
одно
и то же в сопротивлениях ![]() и
и ![]() . Отложим вектор тока
. Отложим вектор тока ![]() на диаграмме (рис.2) в
горизонтальном направлении. Так как напряжение
на диаграмме (рис.2) в
горизонтальном направлении. Так как напряжение ![]() совпадает
по фазе с током
совпадает
по фазе с током ![]() , то направление вектора
, то направление вектора ![]() совпадает с направлением вектора
тока
совпадает с направлением вектора
тока ![]() . Напряжение на индуктивности
. Напряжение на индуктивности ![]() опережает по фазе ток через
индуктивность
опережает по фазе ток через
индуктивность ![]() на угол
на угол ![]() (см. электромагнитная индукция,
правило Ленца, самоиндукция), поэтому вектор
(см. электромагнитная индукция,
правило Ленца, самоиндукция), поэтому вектор ![]() направлен
вдоль вертикальной оси вверх. Сложив векторно
направлен
вдоль вертикальной оси вверх. Сложив векторно ![]() и
и
![]() , получим вектор действующего
напряжения
, получим вектор действующего
напряжения ![]() , модуль которого равен:
, модуль которого равен:
![]() . (9)
. (9)
Полное сопротивление всей цепи ![]() из
(9) равно
из
(9) равно
![]() . (10)
. (10)
По известным значениям напряжения ![]() и полному сопротивлению
и полному сопротивлению ![]() можно найти силу тока
можно найти силу тока ![]()
![]() . (11)
. (11)
Из треугольника сопротивлений (рис.2) можно определить
угол сдвига ![]() , совпадающий с выражением (6).
, совпадающий с выражением (6).
Мгновенная мощность, рассеиваемая в цепи, равна
![]() , (12)
, (12)
и
уже не является синусоидальной величиной (рис.3). Средняя за период активная
мощность ![]() , расходуемая источником на активном
сопротивлении
, расходуемая источником на активном
сопротивлении ![]() ,
равна
,
равна
![]() , (13)
, (13)
где
![]() - действующие значение напряжения в
вольтах,
- действующие значение напряжения в
вольтах, ![]() - действующие значение тока в
амперах,
- действующие значение тока в
амперах, ![]() - коэффициент мощности, где угол
- коэффициент мощности, где угол ![]() определяется формулой (6),
определяется формулой (6), ![]() - активная мощность в ваттах.
- активная мощность в ваттах.
|
|
Величина ![]() называется
кажущейся или полной мощностью. Полная мощность состоит из активной мощности
называется
кажущейся или полной мощностью. Полная мощность состоит из активной мощности ![]() и реактивной мощности
и реактивной мощности ![]() , которая определяется соотношением
, которая определяется соотношением
![]() . (14)
. (14)
Между полной, активной, и реактивной мощностью существует соотношение
![]() . (15)
. (15)
Положительная энергия, поступающая от источника тока к катушке с активным сопротивлением, больше, чем отрицательная энергия, возвращаемая источнику тока. Разность этих энергий равна энергии, поглощаемой активным сопротивлением цепи. Площади, расположенные выше линии времени на рис.3, определяют величину положительной энергии, а расположенные ниже линии времени - величину отрицательной энергии.
Цепь переменного синусоидального тока с активным и емкостным сопротивлением.
Рассмотрим конденсатор, обладающий емкостью ![]() , последовательно соединенный с
активным сопротивлением
, последовательно соединенный с
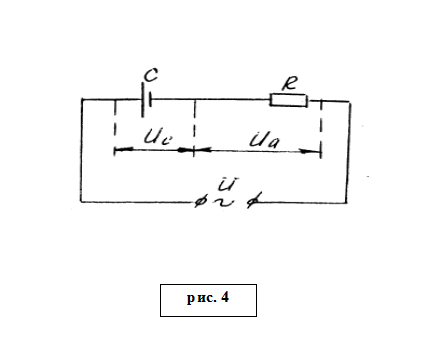
активным сопротивлением ![]() (рис.4).
Колебания частоты
(рис.4).
Колебания частоты ![]() возбуждаются источником
переменной ЭДС
возбуждаются источником
переменной ЭДС ![]() .
.
Дифференциальное уравнение, описывающее колебания тока и напряжения в цепи с активным и емкостным сопротивлениями имеет вид
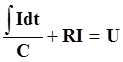 . (16)
. (16)
Алгебраический метод для установившихся вынужденных колебаний в цепи заключается в том, что мы ищем решение уравнения (16) в виде
![]() . (17)
. (17)
Подставляя (17) в уравнение (16), получим:
![]() , (18)
, (18)
![]() , (19)
, (19)
где
![]() играет роль емкостного
сопротивления.
играет роль емкостного
сопротивления.
Метод векторных диаграмм. Пусть в цепи катушки существует переменный синусоидальный ток
![]() . (20)
. (20)
Напряжение ![]() , приложенное к
цепи, одновременно существует на активном
, приложенное к
цепи, одновременно существует на активном
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.