




Лабораторная работа
№5
“ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ И ПОЛУПРОВОДНИКОВ ОТ ТЕМПЕРАТУРЫ”
1. Определить изменение электрического сопротивления металла во время его нагревания.
2. Определить температурный коэффициент электрического сопротивления металла и по его величине установить, что это за металл.
3. Определить изменение электрического сопротивления полупроводника во время его нагревания.
4. Вычислить ширину запрещенной зоны и концентрацию свободных носителей зарядов в полупроводнике при различных температурах.
В зависимости от величины электропроводности кристаллы можно разделить на три класса: диэлектрики, полупроводники и металлы.
Представление о характере и механизмах электропроводности диэлектриков, полупроводников и металлов дает зонная теория твердых тел.
Энергия электронов в отдельном атоме может принимать конкретные дискретные значения. Атом характеризуется своим энергетическим спектром, каждая линия которого соответствует возможному значению энергии. Если несколько атомов объединяются в кристалл, то электронные оболочки атомов перекрываются и из отдельных энергетических уровней соответствующих электронов образовываются полосы уровней, которые называются энергетическими зонами. Зоны, в которых находятся или могут находиться электроны, отделены одна от другой интервалами энергий, которые не может иметь ни один электрон кристалла.
Полностью заполненные зоны называются валентными, частично заполненные зоны - зонами проводимости, а интервал энергий, которые недоступны электронам, - запрещенной зоной или энергетической щелью.
Для того, чтобы кристалл имел минимально возможную энергию, его электроны должны заполнять сначала зону с меньшими энергиями, а потом зону с большими энергиями. В кристалле может реализоваться две принципиально различные ситуации: или все электроны заполняют полностью несколько зон, а остальные зоны остаются свободными, или ж электронов столько, что последняя наиболее энергетическая зона заполнена не полностью.
Кристалл будет изолятором, если последняя зона при ![]() заполнена полностью, иначе -
проводником. Действительно, когда к кристаллу приложить слабое электрическое
поле, то под его влиянием электроны будут ускоряться и переходить в состояние с
большей энергией. Но в изоляторе такой переход невозможен, так как все уровни
энергии заняты, а соответственно с принципом Паули в каждом квантовом состоянии
не может находиться больше, чем один электрон. В проводнике переход возможен,
ибо в зоне проводимости есть свободные энергетические состояния и потому
электрон может изменять свою энергию, упорядочено двигаются в электрическом
поле, создавая электрический ток.
заполнена полностью, иначе -
проводником. Действительно, когда к кристаллу приложить слабое электрическое
поле, то под его влиянием электроны будут ускоряться и переходить в состояние с
большей энергией. Но в изоляторе такой переход невозможен, так как все уровни
энергии заняты, а соответственно с принципом Паули в каждом квантовом состоянии
не может находиться больше, чем один электрон. В проводнике переход возможен,
ибо в зоне проводимости есть свободные энергетические состояния и потому
электрон может изменять свою энергию, упорядочено двигаются в электрическом
поле, создавая электрический ток.
Отметим, что для металлов количество электронов проводимости практически не зависит от температуры.
Рассмотрим случай, когда есть энергетическая щель.
Тогда электроны можно перевести из заполненной зоны в незаполненную, нагревая
кристалл. Такие кристаллы называются собственными полупроводниками. Количество
электронов проводимости, которые перешли в зону проводимости при абсолютной
температуре ![]() пропорциональна
пропорциональна ![]() , где
, где ![]() - ширина энергетической щели,
- ширина энергетической щели, ![]() - константа Больцмана.
- константа Больцмана.
В собственном полупроводнике участие в переносе электрического тока берут не только те электроны, которые вследствие нагревания кристалла пришли из валентной зоны в зону проводимости, освободив некоторый уровень в валентной зоне, но и электроны, которые в валентной зоне получили возможность переходить на освобожденные места. Эти свободные энергетические места в валентной зоне называют дырками. Дырки - это положительно заряженные квазичастицы, которые подчиняются принципу Паули. Поскольку дырок в валентной зоне мало, то проще следить именно за их движением, а не за движением электронов. Количество электронов проводимости и дырок одинаково, ибо кристалл в целом электрически нейтральный. Переход электронов из валентной зоны в свободную возможен в любом диэлектрике, а не только в собственном полупроводнике. Для этого надо преодолеть энергетическую щель в несколько электрон-вольт, то есть диэлектрик надо нагреть практически до температур плавления, ибо только при таких температурах количество электронов проводимости становится ощутимым.
Однако, даже в диэлектрике с большим значением ![]() может возникнуть явление
электропроводности, если в нем есть примеси других атомов. Это связано с тем,
что электронные энергетические уровни атомов-примесей могут попасть в
запрещенную зону диэлектрика.
может возникнуть явление
электропроводности, если в нем есть примеси других атомов. Это связано с тем,
что электронные энергетические уровни атомов-примесей могут попасть в
запрещенную зону диэлектрика.
При этом возможны две ситуации: первая - примесные энергетические уровни заполнены и электроны из них могут перейти в зону проводимости основного вещества, другая - примесные энергетические уровни свободны, поэтому на них могут перейти электроны из валентной зоны, создав в ней квазичастицу или так называемую дырку. В первом случае диэлектрик становится примесным полупроводником донорного типа (n - типа), или электронным полупроводником. Во втором случае кристалл диэлектрика становится полупроводником акцепторного типа (p - типа), или дырочным полупроводником.
Примесные полупроводники можно получить, добавляя другие вещества к собственным полупроводникам. В этом случае в полупроводниках присутствуют как электроны проводимости, так и дырки. Приведем значения ширины энергетической зоны для некоторых полупроводников: Ge (0.7 еВ); донорные полупроводники - ZnSb (0.2 еВ ); Zn (0.01 еВ ); акцепторный полупроводник Zn (0. 014 еВ ).
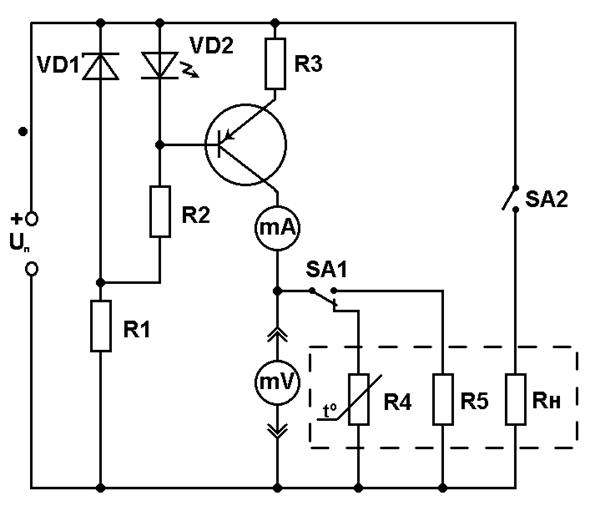 |
Принципиальная схема экспериментальной установки изображена на рис. 1. Она состоит из проводника R4 и полупроводника R3, электропроводность которых исследуется, термостата, нагревателя Rк, стабилизированного источника электроэнергии собранного на элементах R, R1, R2, VD1, VD2, VT1, электроизмерительных приборов.
Используются источник стали напряжения ![]() , миллиамперметр постоянного
тока с
, миллиамперметр постоянного
тока с ![]() = 15 мА, цифровой вольтметр
(рекомендованная точность измерения напряжения - 1мВ; для мультиметра DT830 или
DT920x аналогичная точность достигается в диапазоне 2V ).
= 15 мА, цифровой вольтметр
(рекомендованная точность измерения напряжения - 1мВ; для мультиметра DT830 или
DT920x аналогичная точность достигается в диапазоне 2V ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.