Дослідження властивостей електростатичного поля методом електролітичної ванни (Лабораторна робота № 3)

Лабораторна робота

№3

“ДОСЛІДЖЕННЯ ВЛАСТИВОСТЕЙ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ МЕТОДОМ ЕЛЕКТРОЛІТИЧНОЇ ВАННИ”

ДОСЛІДЖЕННЯ ВЛАСТИВОСТЕЙ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ МЕТОДОМ ЕЛЕКТРОЛІТИЧНОЇ ВАННИ

Мета роботи.

1.  Експериментальним шляхом встановити, розподіл потенціалу електричного поля між двома паралельними пластинами.

2.  Вивчити хід силових ліній електричного поля в електростатичній лінзі.

Вступ.

Електростатичне поле в кожній точці простору може бути описане напруженістю електричного поля  і потенціалом електричного поля , які зв’язані між собою співвідношенням:

(1)

Вектор  - силова характеристика електричного поля, він дорівнює силі, яка діє на одиничний позитивний заряд, що знаходиться в даній точці простору. Потенціал  є енергетичною характеристикою електричного поля і визначає роботу, яку треба виконати зовнішнім силам, щоб перенести одиничний додатній заряд із нескінченності в дану точку простору. Для простоти та наочності використовуються уявлення про силові лінії та поверхні рівного потенціалу. Електричні силові лінії відповідають траєкторіям, вздовж яких почала б рухатися в електричному полі додатно заряджена частинка без урахування її маси. Густина силових ліній в даній області простору пропорційна величині напруженості електричного поля. Вектор  направлений вздовж дотичної до силової лінії. Якщо об’єднати точки простору, які мають однаковий потенціал, то отримаємо еквіпотенціальні поверхні. Силові лінії ортогональні до еквіпотенціальних поверхонь.

З технічної точки зору простіше провести вимірювання скалярного потенціалу електричного поля , ніж вектора напруженості . Особливістю методу електролітичної ванни є те, що використовується не прямий метод вимірювання потенціалу електростатичного поля, а моделювання взаємодії електричних зарядів.

Методика експерименту.

Для моделювання взаємодії статичних електричних зарядів у роботі використовується процес протікання струму в електроліті, де розташовано систему електродів. Ця заміна можлива, якщо підтримувати сталі значення потенціалів на електродах. Доведемо останнє твердження за допомогою закону Ома в диференціальній формі

,                                                                                               (2)

де  - густина електричного струму, і - електропровідність електроліту. Можна вважати, що електроліт  однорідним електропровідником, а  - скаляр і напрямки векторів  та  співпадають. Тому можна вивчити електричне поле електроструму, якщо виміряти розподіл потенціалу електричного поля струму в електроліті. Заміна вивчення електричного поля нерухомих зарядів вивченням поля електричного струму в електроліті дає змогу використовувати металевий зонд для вивчення поля. В електроліті заряди переходять з зонду до розчину. Внаслідок наявності малого електричного струму між зондом та якимось електродом відбувається процес зрівняння потенціалів зонду та точки електроліту, в якій він знаходиться. Щоб цей струм не псував справжню картину електричного поля необхідно, щоб опір електричного кола зонду був набагато більший, ніж опір електроліту. В роботі до електричного кола зонда увімкнений підсилювач вертикального відхилення осцилографа, який має великий вхідний опір . Щоб потенціальна картина поля електричних струмів в електроліті була тотожна до картини поля статичних зарядів, слід підтримувати на електродах стале значення різниці потенціалів. Але при протіканні сталого струму на електродах осідають речовини з розчину електроліту, а це приведе до поляризації електродів. Тому буде викривлена дійсна картина розподілу поля, особливо поблизу електродів. Для запобігання цьому явищу треба подавати на електроди змінну напругу сталої величини.

Покажемо, що в цьому випадку лінії електричного струму в електроліті співпадають з лініями напруженості електричного поля. Потік вектора j через замкнену поверхню S, що обмежує об’єм V дорівнює

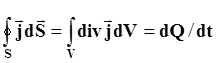,                                                   (3)

де  - електричний заряд, який кожної секунди перетинає поверхню S, що обмежує об’єм V. Для сталого струму . Тому  і, при умові , отримаємо, що . Це рівняння відповідає рівнянню Лапласа для електростатичного поля у вакуумі при відсутності об’ємних зарядів. Крім цього необхідні наступні крайові умови: неперервність струму та потенціалу електричного поля.

Для виконання роботи використовується лабораторний макет, зображений на мал. 1.