








Рекомендации абитуриенту.
Для правильного решения любой предложенной задачи необходимо владеть теоретическим материалом, относящимся к содержанию задачи.
Приступая к решению задачи, вспомните определения и основные свойства величин и понятий, относящиеся к рассматриваемой задаче. Например:
1. Дан прямоугольный треугольник, следовательно, …
2. Требуется решить неравенство: решением неравенства называется…. Затем вспомнить основные свойства неравенств и т.д.
3. Окружность описана около прямоугольного треугольника, следовательно, …
4. Решить неравенство с модулем: надо разбить числовую ось на отдельные промежутки, в каждом из которых предложенное неравенство не содержит знака абсолютной величины и т.д.
5. Требуется решить логарифмическое (показательное) уравнение. Вспомните основные свойства логарифмической (показательной) функции и посмотрите, какие из них разумно использовать.
Если нужно сделать чертеж, то следует сделать его в соответствии с условиями задачи. Хороший чертеж – помощник в решении задачи, он может подсказать правильный способ решения задачи.
При решении уравнения сравните между собой все входящие в уравнение величины, попробуйте найти что-то общее между ними или установите связь между некоторыми из них.
При решении тренировочных задач запоминайте использованные способы и специальные приемы, которые позволили решить задачу.
![]() Образцы вариантов
задач по математике, предлагавшихся на вступительных письменных испытаниях в
СЗТУ в 2005 году
Образцы вариантов
задач по математике, предлагавшихся на вступительных письменных испытаниях в
СЗТУ в 2005 году
ВАРИАНТ 1
2. Решить уравнение ![]()
3. Доказать тождество
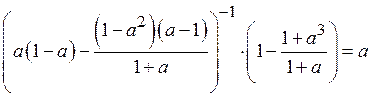 .
.
4. В равнобедренный треугольник, длина основания которого равна 3 см, а длина высоты 6 см, вписан квадрат, сторона которого лежит на основании, а противоположные вершины на боковых сторонах. Найти длину стороны квадрата.
5. Решить неравенство ![]() где
где 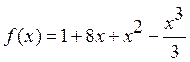 .
.
ВАРИАНТ 2
2. Решить уравнение ![]()
3. Доказать тождество
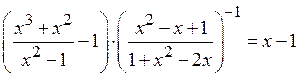 .
.
4. Стороны основания прямого параллелепипеда образуют угол, равный 600, а их длины равны 8 см и 15 см. Меньшая из площадей диагональных сечений равна 130 см2. Найти площадь боковой поверхности параллелепипеда.
5. Решить систему уравнений
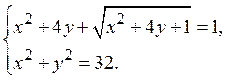
Решения задач предложенных вариантов
ВАРИАНТ 1
Решение. Область определения уравнения задается
системой неравенств 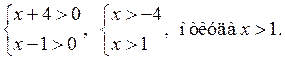 Применяя
свойства логарифмов
Применяя
свойства логарифмов ![]() получаем
получаем ![]() , откуда
, откуда ![]() или
или ![]() .
.
Корни последнего квадратного уравнения ![]() .
.
![]()
Второй корень ![]() не
входит в ООУ.
не
входит в ООУ.
Ответ: ![]()
2. Решить уравнение ![]()
Решение. Делим обе части уравнения на ![]() . Уравнение
приобретает вид
. Уравнение
приобретает вид ![]() . Делаем
замену переменных
. Делаем
замену переменных ![]() . Получаем
квадратное уравнение
. Получаем
квадратное уравнение ![]() .
Корни квадратного уравнения
.
Корни квадратного уравнения ![]() .
.
![]() .
Значение
.
Значение ![]() не подходит, т.к.
не подходит, т.к. ![]() .
.
Возвращаемся к исходной переменной: ![]() , следовательно,
, следовательно, ![]()
Ответ: ![]() .
.
3. Доказать тождество
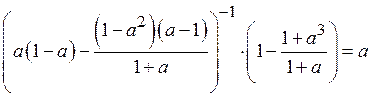 .
.
Решение. Преобразуем левую часть. Упростим первую
скобку, используя формулу сокращенного умножения ![]() . Во второй скобке
используем формулу сокращенного умножения
. Во второй скобке
используем формулу сокращенного умножения ![]() .
.
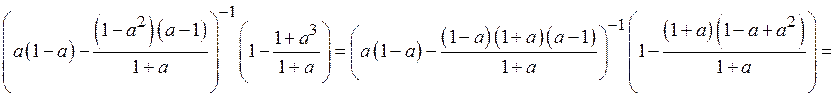
![]() . Используя
определение степени с отрицательным показателем, будем иметь
. Используя
определение степени с отрицательным показателем, будем иметь ![]() .
.
Тождество доказано.
4. В равнобедренный треугольник, длина основания которого равна 3 см, а длина высоты 6 см, вписан квадрат, сторона которого лежит на основании, а противоположные вершины на боковых сторонах. Найти длину стороны квадрата.
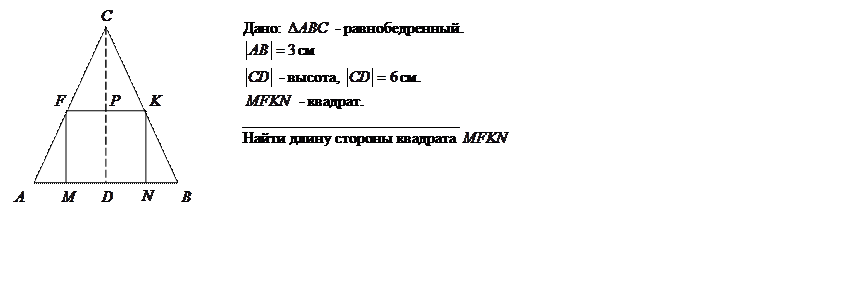
Решение.
1 способ. Обозначим длину стороны
квадрата через ![]() . Треугольники
. Треугольники
![]() и
и ![]() подобны, т.к.
подобны, т.к. ![]() параллельна
параллельна ![]() и, следовательно,
справедливо равенство
и, следовательно,
справедливо равенство
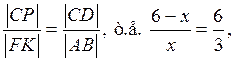
откуда следует ![]() , или окончательно
, или окончательно ![]() .
.
2 способ. Площадь
треугольника равна ![]() , где
, где ![]() - основание
треугольника,
- основание
треугольника, ![]() высота,
опущенная на основание. Тогда площадь треугольника
высота,
опущенная на основание. Тогда площадь треугольника ![]() .
.
Обозначим длину стороны квадрата ![]() . Площадь квадрата
. Площадь квадрата ![]() .
.
Теперь заметим, что площадь треугольника ![]() можно представить в
виде
можно представить в
виде ![]() .
.
Найдем площадь каждого из трех треугольников:
![]() ;
;
![]() , ясно, что
, ясно, что
![]() , тогда
, тогда
![]() ,
,
![]() , причем
, причем ![]() , отсюда следует, что
, отсюда следует, что
![]() .
.
Подставим найденные площади трех треугольников и квадрата в
формулу для определения площади данного треугольника ![]()
![]() .
.
Упростим полученное выражение:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.