После приведения подобных членов получим
![]() или
или ![]() . Отсюда следует
. Отсюда следует ![]() .
.
Ответ: Сторона квадрата ![]() см.
см.
5. Решить неравенство ![]() где
где 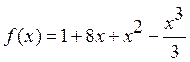 .
.
Решение. Найдем производную ![]() . Тогда данное
неравенство примет вид
. Тогда данное
неравенство примет вид
![]() .
.
Следует рассматривать только те значения ![]() , при которых
, при которых ![]() или, что то же
самое,
или, что то же
самое, ![]() . Решим последнее
неравенство с помощью метода интервалов, для чего найдем сначала корни
уравнения
. Решим последнее
неравенство с помощью метода интервалов, для чего найдем сначала корни
уравнения ![]()
![]() , т.е.
, т.е. ![]()
![]() Запишем последнее
неравенство в виде
Запишем последнее
неравенство в виде ![]() и нанесем
критические очки
и нанесем
критические очки ![]() и
и ![]() на числовую ось. Вся
числовая ось разбивается на три интервала, причем в самих этих
на числовую ось. Вся
числовая ось разбивается на три интервала, причем в самих этих
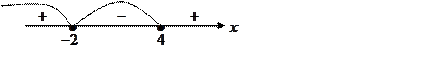
точках неравенство выполняется.
Если ![]() , то оба множителя
положительны и, следовательно, левая часть положительна и на рисунке
над интервалом
, то оба множителя
положительны и, следовательно, левая часть положительна и на рисунке
над интервалом ![]() ставим
знак “плюс”. После перехода через точку
ставим
знак “плюс”. После перехода через точку ![]() лишь один из
множителей меняет знак и, следовательно, над интервалом
лишь один из
множителей меняет знак и, следовательно, над интервалом ![]() ставим знак “минус”.
Наконец, для всех
ставим знак “минус”.
Наконец, для всех ![]() оба
множителя отрицательны и, следовательно, над интервалом
оба
множителя отрицательны и, следовательно, над интервалом ![]() ставим знак “плюс”.
ставим знак “плюс”.
Итак, неравенство ![]() выполняется для всех
выполняется для всех
![]() из промежутка
из промежутка ![]() .
.
Обращаясь к данному неравенству, рассмотрим два случая:
1)
Пусть ![]() , т.е.
, т.е. ![]() . Тогда обе части данного
неравенства положительны и, возведя их в квадрат, получим
. Тогда обе части данного
неравенства положительны и, возведя их в квадрат, получим ![]() или
или ![]() которое равносильно
неравенству
которое равносильно
неравенству ![]() . Решим это
неравенство с помощью метода интервалов, для чего сначала найдем корни
уравнения
. Решим это
неравенство с помощью метода интервалов, для чего сначала найдем корни
уравнения ![]() . Будем иметь:
. Будем иметь: ![]() , так что
, так что ![]() . Неравенство
. Неравенство ![]() запишем в виде
запишем в виде ![]() . Числовая ось
разбивается точками
. Числовая ось
разбивается точками ![]() и
и ![]() на 3 интервала
на 3 интервала ![]() , над каждом из
которых ставим соответственно знаки “плюс”, ”минус” и “плюс”. Итак, неравенство
, над каждом из
которых ставим соответственно знаки “плюс”, ”минус” и “плюс”. Итак, неравенство
![]() выполняется в
интервале
выполняется в
интервале ![]() , но т.к. в
рассматриваемом случае
, но т.к. в
рассматриваемом случае ![]() , то
, то
![]()
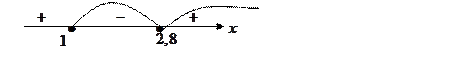
исходное неравенство выполняется
для всех ![]() из промежутка
из промежутка ![]() .
.
2) Пусть ![]() . Тогда левая часть
данного неравенства всегда положительна, а правая часть отрицательная или ноль
и, следовательно, оно верно при всех
. Тогда левая часть
данного неравенства всегда положительна, а правая часть отрицательная или ноль
и, следовательно, оно верно при всех ![]() ,
но т.к. выражение, стоящее под корнем, положительно или ноль только для
,
но т.к. выражение, стоящее под корнем, положительно или ноль только для ![]() из промежутка
из промежутка ![]() , то в этом случае
решением исходного неравенства будет промежуток
, то в этом случае
решением исходного неравенства будет промежуток ![]() . Объединяя пункты 1)
и 2), получим окончательно решением данного неравенства является промежуток
. Объединяя пункты 1)
и 2), получим окончательно решением данного неравенства является промежуток ![]() .
.
Ответ: ![]() .
.
ВАРИАНТ 2
Решение. Область определения уравнения задается системой неравенств
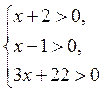 или
или 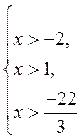
![]()
Применяя свойство логарифмов ![]() получаем
получаем ![]() , откуда
, откуда ![]() или
или ![]() .
.
Найдем корни этого квадратного
уравнения ![]() .
.
![]()
Второй корень ![]() не входит в ООУ.
не входит в ООУ.
Ответ: ![]()
2. Решить уравнение ![]()
Решение. Делим обе части уравнения на ![]() . Уравнение
приобретает вид
. Уравнение
приобретает вид ![]() или
или ![]() . Делаем замену
переменных
. Делаем замену
переменных ![]() . Получаем
квадратное уравнение
. Получаем
квадратное уравнение ![]() . Корни
квадратного уравнения
. Корни
квадратного уравнения ![]() .
.
![]() .
Значение
.
Значение ![]() не подходит,
т.к.
не подходит,
т.к. ![]() .
.
Возвращаемся к исходной переменной: ![]() отсюда
отсюда ![]() , а тогда
, а тогда ![]()
Ответ: ![]() .
.
3. Доказать тождество
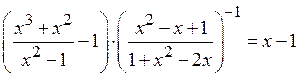 .
.
Решение. Преобразуем левую
часть тождества. В первой скобке приведем дроби к общему знаменателю. Во второй
скобке используем определение степени с отрицательным показателем и формулу
сокращенного умножения ![]() .
.
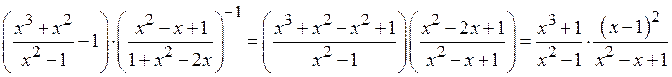 .
.
Теперь применим формулы
сокращенного умножения ![]() ,
,
![]() . Тогда получим
. Тогда получим
![]()
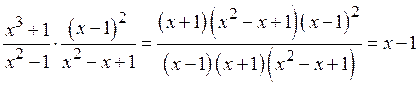 .
.
Тождество доказано.
4. Стороны основания прямого параллелепипеда образуют угол, равный 600, а их длины равны 8 см и 15 см. Меньшая из площадей диагональных сечений равна 130 см2. Найти площадь боковой поверхности параллелепипеда.
Решение. На рисунке изображен параллелепипед ![]() .
. 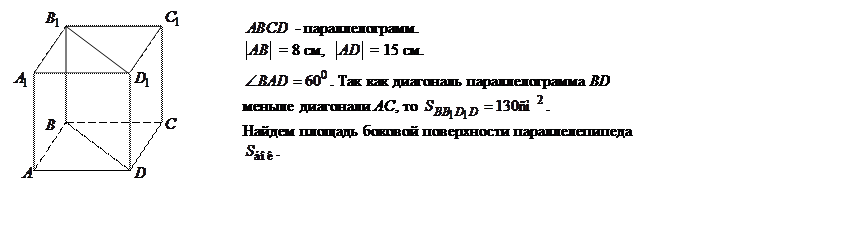
Рассмотрим ![]() .
По теореме косинусов
.
По теореме косинусов ![]() , т.е..
, т.е..
![]() . Отсюда
. Отсюда ![]() . Т.к. по условию
параллелепипед прямой, то диагональное сечение
. Т.к. по условию
параллелепипед прямой, то диагональное сечение ![]() - прямоугольник.
Найдем площадь этого прямоугольника
- прямоугольник.
Найдем площадь этого прямоугольника ![]() ,
тогда
,
тогда ![]() .
.
Площадь боковой поверхности параллелепипеда ![]()
![]() .
.
Ответ: ![]() .
.
5. Решить систему уравнений
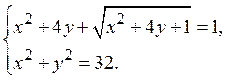
Решение. Введем новую
переменную ![]() , тогда
, тогда ![]() . Первое уравнение
примет вид
. Первое уравнение
примет вид ![]() или
или ![]() .
.
Т.к. ![]() , то должно быть
, то должно быть ![]() и обе части
последнего равенства при этом положительны.
и обе части
последнего равенства при этом положительны.
Возведем обе части в квадрат, получим:
![]() или
или ![]() .
.
Найдем корни этого квадратного
уравнения ![]() .
.
Корень ![]() не подходит, т.к.
должно быть
не подходит, т.к.
должно быть ![]() . Получили
. Получили ![]() . Следовательно,
. Следовательно, ![]() или
или ![]() .
.
Тогда система примет вид
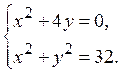
Решим данную систему методом
подстановки: из первого уравнения ![]() ,
тогда
,
тогда ![]() и, подставив во
второе уравнение, получим:
и, подставив во
второе уравнение, получим:
![]() или
или ![]() .
.
Найдем корни полученного
уравнения: ![]() .
.
Значение ![]() не
подходит, т.к.
не
подходит, т.к. ![]() .
.
Следовательно, ![]() ;
а тогда
;
а тогда ![]() , откуда следует
, откуда следует ![]() .
.
Ответ: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.