




Образец теста по математике, предлагаемого на вступительных испытаниях в СЗТУ в 2005 году
1. Вычислить 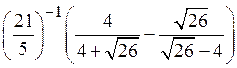 .
.
2. Упростить выражение ![]() .
.
3. Решить уравнение ![]() .
.
4. Решить неравенство ![]() .
.
5. Решить систему уравнений 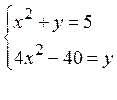 .
.
6. Решить уравнение ![]() .
.
7. Решить неравенство ![]() .
.
8. Решить неравенство 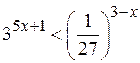 .
.
9. Вычислить ![]() .
.
10. Решить уравнение ![]() .
.
11. Построить графики функций 1)![]() и 2)
и 2)![]() . Определить количество
точек, в которых эти графики пересекаются.
. Определить количество
точек, в которых эти графики пересекаются.
12. Найти все корни уравнения ![]() , расположенные в
промежутке
, расположенные в
промежутке ![]() .
.
13. Упростить выражение ![]() .
.
14. Найти радиус круга, если проведенная в этом круге хорда длиной 24см удалена от центра круга на 16см.
15. Найти область определения
функции ![]() .
.
16. Сумма первых двух членов арифметической прогрессии равна 10, а пятый член равен 26. Чему равен первый член и разность этой прогрессии?
Предложенный тест по математике рекомендуется абитуриенту решить самостоятельно.
Для проверки правильности ответов ниже приводим ответы и решения всех задач теста.
Решения задач предложенного теста
Задача 1. Вычислить  .
.
Решение. Используя определение степени с отрицательным показателем и приводя разность к общему знаменателю, получим
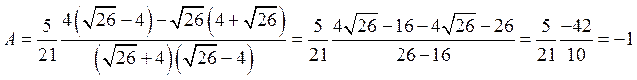
Ответ: ![]() .
.
Задача 2. Упростить
выражение ![]() .
.
Решение. Заметим, что ![]() , а
, а ![]()
Тогда данное выражение примет вид: 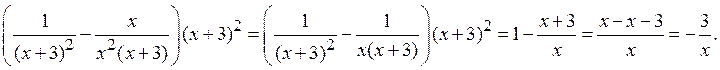
Ответ: ![]() .
.
Задача 3. Решить уравнение
![]() .
.
Решение. Так как ![]() стоящее в знаменателе
дроби равно нулю при
стоящее в знаменателе
дроби равно нулю при ![]() то будем
считать, что
то будем
считать, что ![]() . Запишем данное
уравнение в виде
. Запишем данное
уравнение в виде ![]() .
.
После приведения к общему знаменателю получим
![]()
или
![]() .
.
Приравниваем к нулю числитель
дроби и находим корни уравнения: ![]()
Ответ: ![]()
Задача 4. Решить
неравенство ![]() .
.
Решение. Раскрываем скобки
и приводим подобные члены в обоих частях неравенства: ![]() . Будем иметь
. Будем иметь ![]() или
или ![]() .
.
Ответ: ![]()
Задача 5. Решить систему
уравнений 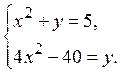
Решение. Заменим в первом
уравнении величину ![]() соответствующим
выражением из второго уравнения. Получим равносильную систему
соответствующим
выражением из второго уравнения. Получим равносильную систему 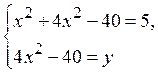 или
или 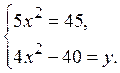
Из первого уравнения имеем ![]() , а тогда из второго
уравнения получаем, что
, а тогда из второго
уравнения получаем, что ![]() .
.
Ответ: 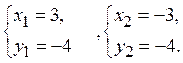
Задача 6. Решить уравнение
![]() .
.
Решение. Возведем обе
части иррационального уравнения в квадрат и найдем корни полученного
квадратного уравнения: ![]()
![]() .
.
После приведения подобных членов
получим ![]()
![]()
Корнями этого уравнения являются ![]()
Проверим, являются ли эти числа корнями исходного уравнения:
1) ![]() Равенство верно,
значит,
Равенство верно,
значит, ![]() - корень уравнения.
- корень уравнения.
2) ![]() Значит,
Значит, ![]() не является корнем
исходного уравнения.
не является корнем
исходного уравнения.
Ответ: ![]()
Задача 7. Решить
неравенство ![]() .
.
Решение. Данное
неравенство ![]() равносильно
неравенству
равносильно
неравенству ![]() или
или ![]() . Разделив все части
полученного неравенства на
. Разделив все части
полученного неравенства на ![]() и
меняя знаки неравенств, получим
и
меняя знаки неравенств, получим ![]() .
.
Ответ: ![]() .
.
Задача 8. Решить
неравенство 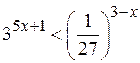 .
.
Решение. Так как ![]() то данное неравенство можем
записать в виде
то данное неравенство можем
записать в виде ![]() или в таком
виде
или в таком
виде ![]() .
.
Функция ![]() возрастающая, так как
возрастающая, так как ![]() Следовательно,
полученное неравенство, а, значит, и исходное равносильно неравенству
Следовательно,
полученное неравенство, а, значит, и исходное равносильно неравенству
![]()
или
![]() , значит, и исходное равносильно
неравенству
, значит, и исходное равносильно
неравенству
![]()
или
![]()
Ответ: ![]()
Задача 9. Вычислить ![]() .
.
Решение. Замечая, что ![]() и, используя основное
логарифмическое тождество
и, используя основное
логарифмическое тождество ![]() , можем
написать
, можем
написать 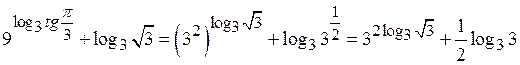 .
.
Учитывая, что ![]() ,
будем иметь
,
будем иметь
![]() .
.
Ответ: ![]()
Задача 10. Решить
уравнение ![]() .
.
Решение. Решаем уравнение
при ![]() Используя равенства
Используя равенства ![]()
![]() запишем данное
уравнение в виде
запишем данное
уравнение в виде ![]()
или в таком виде ![]() , т.е.
, т.е. ![]() Отсюда
Отсюда ![]()
Ответ: ![]()
Задача 11. Построить графики функций 1) ![]() и 2)
и 2)![]() . Определить количество
то
. Определить количество
то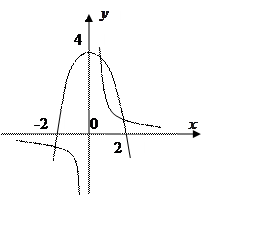 чек, в которых эти
графики пересекаются.
чек, в которых эти
графики пересекаются.
Решение. Графики функций:
1) ![]() - парабола; 2)
- парабола; 2) ![]() - гипербола. Как видно
из рисунка, графики заданных функций пересекаются в трех точках.
- гипербола. Как видно
из рисунка, графики заданных функций пересекаются в трех точках.
Ответ: ![]()
Задача 12. Найти все корни
уравнения ![]() , расположенные в
промежутке
, расположенные в
промежутке ![]() .
.
Решение. Вынесем за скобку
![]()
![]() Выражение
Выражение ![]() так как при любом
так как при любом ![]() выполняется
неравенство
выполняется
неравенство ![]() Уравнение
Уравнение ![]() имеет корни:
имеет корни: ![]() где
где ![]() Подставляя в выражение
Подставляя в выражение
![]() вместо
вместо ![]() целые числа
целые числа ![]() получаем значения
получаем значения ![]() и т.д. Из них
промежутку
и т.д. Из них
промежутку ![]() принадлежат
принадлежат ![]() и
и ![]() .
.
Ответ: ![]()
Задача 13. Упростить
выражение ![]() .
.
Решение. Учитывая, что ![]() ,
, ![]() , а
, а ![]() , можем написать
, можем написать 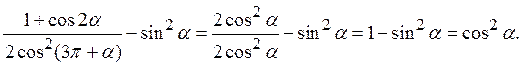
Ответ: ![]()
Задача 14. Найти радиус круга, если проведенная в этом круге хорда длиной 24см удалена от центра круга на 16см.
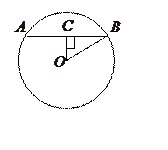 Решение. В
окружности проведем хорду
Решение. В
окружности проведем хорду ![]() ,
длина которой равна 24см.
,
длина которой равна 24см. ![]() -
центр круга,
-
центр круга, ![]() и длина
и длина ![]() равна 16см, а точка
равна 16см, а точка ![]() делит хорду
делит хорду ![]() пополам.
пополам. ![]() - прямоугольный.
- прямоугольный. ![]() см,
см, ![]() см. По теореме Пифагора
см. По теореме Пифагора
![]()
Ответ: Длина радиуса круга равна 20см.
Задача 15. Найти область
определения функции ![]() .
.
Решение. Область определения заданной функции находим, исходя из следующих соображений:
1). Из множества действительных
чисел исключим те значения ![]() при
котором знаменатель обращается в нуль, т.е.
при
котором знаменатель обращается в нуль, т.е. ![]()
2). Так как в числителе дроби корень четной степени, то подкоренное выражение должно быть больше или равно нулю.
Итак: ![]() , отсюда
, отсюда
![]()
Ответ: ![]() .
.
Задача 16. Сумма первых двух членов арифметической прогрессии равна 10, а пятый член равен 26. Чему равен первый член и разность этой прогрессии?
Решение. В согласии с
условием задачи можем написать ![]() ,
, ![]() . Используем формулу
общего члена арифметической прогрессии:
. Используем формулу
общего члена арифметической прогрессии: ![]() где
где ![]() - первый член,
- первый член, ![]() - разность прогрессии.
Тогда справедливы два равенства:
- разность прогрессии.
Тогда справедливы два равенства:
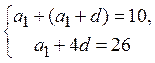 или
или 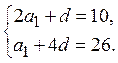
Решая систему, находим ![]()
Ответ: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.