Математика \ Математическая статистика

Вычисление коэффициента ранговой корреляции Спирмена

Страницы работы

3 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Вариант 3.

I. Независимость признаков

По оценкам девяти судей сумма мест 10-ти сильнейших пар в танцах на льду распределились так:

Страна	Rus1	Fr1	Rus2	Ger1	Can	GB	USA	Fr2	Rus3	Ger2
Техника	9	17	29	40	42	52	64	71	82	87
Артистичность	17	16	29	40	37	53	61	74	81	87

Есть ли связь между техническим мастерством и красотой исполнения.? (). Критическое значение для коэф. Спирмена 0.564.

Решение. Вычислим коэффициент ранговой корреляции Спирмена по следующей формуле:

, где - объем выборки, - разность между парами рангов для -го объекта.

Составляем таблицу с рангами:

Страна	Rus1	Fr1	Rus2	Ger1	Can	GB	USA	Fr2	Rus3	Ger2
Техника	9	17	29	40	42	52	64	71	82	87
Артистичность	17	16	29	40	37	53	61	74	81	87
Ранг 1	1	2	3	4	5	6	7	8	9	10
Ранг 2	2	1	3	5	4	6	7	8	9	10
	-1	1	0	-1	1	0	0	0	0	0
	1	1	0	1	1	0	0	0	0	0

Получаем: .

Проверим значимость коэффициента. Вычислим значение критерия: .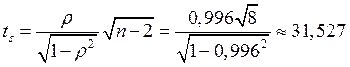

Так как , гипотезу значимости коэффициента следует отвергнуть, связь между техническим мастерством и красотой исполнения подтверждается на данном уровне значимости.

Тот же самый результат получается, если сравнить вычисленный коэффициент ранговой корреляции с критическим значением 0,564.

II. Сравнение «результатов обработки»

У двух группы испытуемых проверяли время реакции на свет и звук. Результаты представлены в следующей таблице.

Испытуемый

Время в миллисекундах (звук)

Время в миллисекундах (свет)

223

181

164

194

209

173

183

153

180

168

Является ли время реакции одинаковым? Выборки предполагаются нормальными. Парные данные.

Решение. Обозначим первую выборку (время реакции на звук) , вторую выборку (время реакции на свет) . Найдем выборочные числовые характеристики выборок.


	223	973,44
	164	772,84
	209	295,84
	183	77,44
	180	139,24

Сумма	959	2258,8

Выборочное среднее .

Выборочная исправленная дисперсия .


	181	51,84
	194	408,04
	173	0,64
	153	432,64
	168	33,64

Сумма	869	926,8

Выборочное среднее .

Выборочная исправлена дисперсия .

Исправленные дисперсии различны, поэтому проверим гипотезу о равенстве дисперсий, используя критерий Фишера-Снедекора. Найдем отношение большей дисперсии к меньшей:

Дисперсия значительно больше дисперсии , поэтому в качестве конкурирующей гипотезы примем гипотезу . По таблице при уровне значимости и числам степеней свободы и найдем критическую точку . Так как , нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий.

Итак, предположение о равенстве генеральных дисперсий выполняется, поэтому сравним средние. Введем нулевую гипотезу: при конкурирующей гипотезе.

Вычислим наблюдаемое значение критерия по формуле:

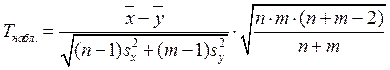Получаем:

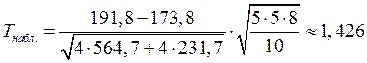Находим критическую точку (двусторонняя критическая область) из таблицы Стьюдента при уровне значимости и числу степеней свободы . Так как наблюдаемое значение критерия 1,426 меньше критического, нет оснований отвергнуть нулевую гипотезу, то есть среднее время реакции на свет и на звук одинаково.