Основные законы электростатики и постоянного тока: Методические указания и контрольные задания к контрольной работе № 3 по физике. Часть 1, страница 3

7. Электроемкость (емкость) C  уединенного (т.е. такого, на который не действуют внешние электростатические поля) проводника, заряженного зарядом q и поэтому обладающего потенциалом f относительно бесконечности:

C=q/f  .                                      (11)

Емкость уединенного проводящего шара (сферы) радиуса R:

C=4pe₀eR  .                                           (12)

8. Система из двух проводников, заряженных равными по величине и противоположными по знаку зарядами q, называется конденсатором. Емкость C конденсатора:

C=q/U  ,                                               (13)

где U – разность потенциалов между обкладками;

а) eмкость плоского конденсатора с расстоянием между обкладками d, малыми по сравнению с характерным размером перекрывающейся части пластин

C=e₀eS/d  ,        (14)

где S – площадь перекрывающейся части обкладок конденсатора (рис.1);

б) eмкость сферического конденсатора с радиусами внешней и внутренней обкладок R₂ и R₁ , имеющих общий центр:

C=4pe₀e R₁R₂ /(R₂ – R₁ ) ;                         (15)

в) eмкость цилиндрического конденсатора (или коаксиального кабеля) длиной L с радиусами внешней и внутренней обкладок R₂ и R₁ , имеющих общую ось

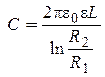  .                                       (16)

9. Система из двух равных по величине и противоположных по знаку зарядов +q и –q, расположенных на расстоянии d, малом по сравнению с расстоянием r до точки, в которой определяются напряженность и потенциал поля этой системы, называется электрическим диполем. Электрический момент диполя определяется как

  .                                          (17)

Вектор направлен от отрицательного заряда к положительному, напряженность E и потенциал f  поля диполя:

  .   (18)

10. Поляризованность P помещенного во внешнее электрическое поле E диэлектрика, определяемая как дипольный момент (17) единицы объема, прямо пропорциональна напряженности

  ,                               (19)

где c – диэлектрическая восприимчивость вещества.

11. Электрическая индукция (электрическое смещение) D диэлектрика

  ,                               (20)

где

e = 1+c   –                                            (21)

диэлектрическая проницаемость среды.

12. Теорема Гаусса. Поток вектора индукции электрического поля через произвольную замкнутую поверхность S равен алгебраической сумме свободных зарядов , охватываемых этой поверхностью 

 .                                  (22)

Другая, эквивалентная (с учетом (20)) формулировка теоремы для потока вектора напряженности электрического поля

,                    (23)

где  – связанные заряды, охватываемые поверхностью S .

13. Плотность энергии электрического поля w – энергия единицы объема пространства, занятого полем

.               (24)

14. Энергия конденсатора емкости C

,                        (25)

где q – заряд на обкладках конденсатора, U – разность потенциалов между обкладками.

Постоянный ток

15. Плотность тока  j – это заряд, протекающий в единицу времени через единицу площади проводника, перпендикулярную к направлению упорядоченного движения носителей тока

.                                    (26)