








|
5.1. Эффективность газовых завес
при обтекании адиабатической
поверхности
|
дной из проблем теплофизики является защита обтекаемых
поверхностей от воздействия высокотемпературных и химически агрессивных потоков газа. Во многих случаях весьма эффективными могут быть гидродинамические методы защиты, когда охлаждающий газ (или жидкость) вдувается в пограничный слой через защищаемую поверхность. Не всегда можно распределить вдуваемый газ равномерно по большой площади и сохранить достаточную прочность стенки, поэтому более простым методом заградительного охлаждения является локальный вдув через небольшие пористые участки, тангенциальные щели или интенсивное охлаждение начального участка проницаемой стенки.
В литературе указанные методы защиты называются по-разному: заградительное, струйное или пленочное охлаждение, тепловые или газовые завесы.
Рассмотренный здесь метод основан на асимптотической теории турбулентного пограничного слоя, развивающегося на адиабатической и неадиабатической поверхностях.
Различные схемы организации газовых завес основываются на использовании одного из следующих способов тепловой защиты (рис. 5.1):
а) охлаждение предвключенного непроницаемого участка;
б) вдув охладителя через начальный пористый участок;
в) подача охладителя через тангенциальную щель.
Основным параметром, которым оценивается эффективность газовой завесы, является безразмерная относительная температура
теплоизолированной стенки:
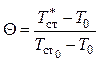 .
.
Этот параметр так и называется – эффективность газовой завесы. Найдем распределение температуры адаибатической стенки по длине пластины.
|
|
|
|
|
|
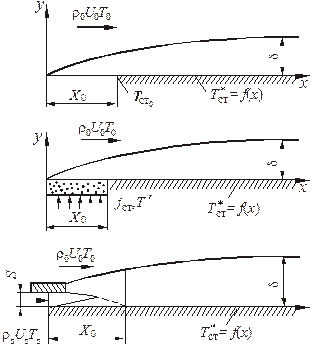
Рис. 5.1. Схемы основных вариантов организации
газовых завес
Интегральное уравнение энергии на плоской непроницаемой пластине
![]() .
(5.1)
.
(5.1)
Поскольку
поверхность адиабатическая, ![]() ,
,
![]() и уравнение
(5.1) имеет вид
и уравнение
(5.1) имеет вид
![]() (5.2)
(5.2)
или
![]() ,
,
![]() ,
,
![]() ,
,
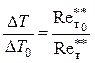 ,
,
где ![]() ,
, ![]() ,
,
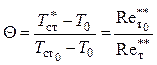 ,
(5.3)
,
(5.3)
где ![]() – число
Рейнольдса в начальном сечении адиабатической пластины;
– число
Рейнольдса в начальном сечении адиабатической пластины; ![]() – число
Рейнольдса в текущем сечении адиабатической пластины. Число
– число
Рейнольдса в текущем сечении адиабатической пластины. Число ![]() находится из
решения интегрального уравнения энергии участка охлаждения (см. схемы организации завес).
находится из
решения интегрального уравнения энергии участка охлаждения (см. схемы организации завес).
На
участке ![]() при
при ![]() выполняется
условие
выполняется
условие
![]() ,
,
![]() .
.
В области ![]() подобие
динамического и теплового пограничных слоев нарушается, так как изменяются
граничные условия на адиабатической поверхности пластины. Внутри
пограничного слоя происходит выравнивание температур только вследствие
турбулентного перемешивания и подсоса массы газа из внешнего потока. При этом
наибольшая интенсивность перемешивания имеет место в пристенной области, где
производная
подобие
динамического и теплового пограничных слоев нарушается, так как изменяются
граничные условия на адиабатической поверхности пластины. Внутри
пограничного слоя происходит выравнивание температур только вследствие
турбулентного перемешивания и подсоса массы газа из внешнего потока. При этом
наибольшая интенсивность перемешивания имеет место в пристенной области, где
производная ![]() максимальна.
В результате деформация профиля температур происходит таким образом, что
область с
максимальна.
В результате деформация профиля температур происходит таким образом, что
область с ![]() непрерывно
увеличивается, т. е. растет область, где
непрерывно
увеличивается, т. е. растет область, где ![]() . Одновременно
вследствие подсоса газа из внешнего потока температура в пограничном слое
приближается к температуре
. Одновременно
вследствие подсоса газа из внешнего потока температура в пограничном слое
приближается к температуре ![]() ,
т. е. при
,
т. е. при ![]()
![]() .
(5.4)
.
(5.4)
Развитие теплового пограничного слоя на адиабатической стенке, охлаждаемой завесой, показано на рис. 5.2.
|
|
|
|
|
|
|
|
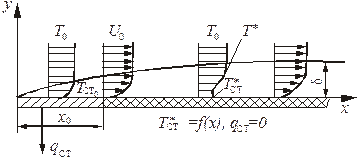
Рис. 5.2. Вырождение теплового пограничного слоя
на адиабатической поверхности в условиях завесы
Поскольку теплообмен через стенку
отсутствует (стенка адиабатическая), можно записать, что 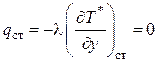 , откуда следует
, откуда следует
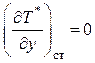 , или на
некотором расстоянии от стенки
, или на
некотором расстоянии от стенки ![]() .
Это означает, что у стенки имеется участок, где температура в пограничном слое
постоянна.
.
Это означает, что у стенки имеется участок, где температура в пограничном слое
постоянна.
Запишем выражение для толщины потери энергии пограничного слоя постоянных физических свойств
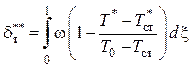 .
.
Учитывая (5.4), на
адиабатической поверхности при ![]() получим
получим
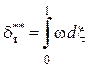 .
.
Тогда отношение толщины потери энергии на адиабатической стенке с учетом деформации профиля температуры к толщине потери импульса будет иметь вид
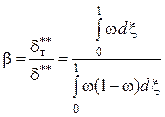 .
.
Принимая
во внимание, что ![]() ,
получаем
,
получаем ![]() – коэффициент,
учитывающий деформацию поля температур.
– коэффициент,
учитывающий деформацию поля температур.
При ![]()
![]() , а при
, а при ![]()
![]() . Тогда уравнение
(5.3) имеет вид
. Тогда уравнение
(5.3) имеет вид
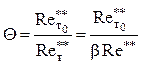 .
(5.5)
.
(5.5)
Число
Рейнольдса ![]() находится из
решения интегрального уравнения импульсов
находится из
решения интегрального уравнения импульсов
![]() ,
,
где коэффициент трения
![]() .
.
При
течении газа на пластине (![]() ,
,
![]() ) уравнение
импульсов будет иметь вид
) уравнение
импульсов будет иметь вид
![]() ,
,
где ![]() ,
, ![]() .
.
В результате интегрирования уравнения импульсов имеем
![]() .
(5.6)
.
(5.6)
Подставляем (5.6) в (5.5):
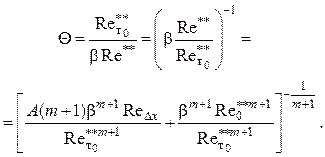 (5.7)
(5.7)
Поскольку
на участке ![]()
![]() ,
, ![]() и
и ![]() ,
а коэффициент
,
а коэффициент ![]() ,
получаем из (5.7)
,
получаем из (5.7)
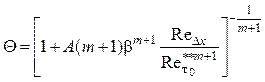 .
(5.8)
.
(5.8)
Для развитого
турбулентного пограничного слоя со степенным профилем скорости ![]() :
: ![]() ,
, ![]() ,
, ![]() , тогда
, тогда
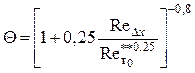 .
(5.9)
.
(5.9)
Начальное число
Рейнольдса ![]() в сечении
в сечении ![]() находим в зависимости
от способа организации завесы путем решения интегрального уравнения энергии на
участке
находим в зависимости
от способа организации завесы путем решения интегрального уравнения энергии на
участке ![]() .
.
1. При вдуве охладителя через тангенциальную щель
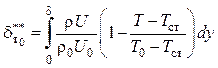 .
.
В сечении
щели ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
поэтому
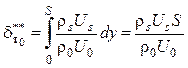 ,
,
откуда
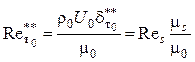 .
.
Тогда (5.9) будет иметь вид
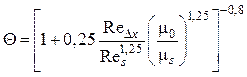 ,
(5.10)
,
(5.10)
где ![]() ,
, ![]() – высота
щели.
– высота
щели.
2. При охлаждении начального непроницаемого участка
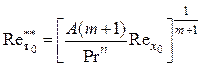 , где
, где ![]() ,
,
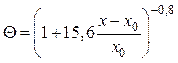 .
(5.11)
.
(5.11)
3. При вдуве через пористый участок число Рейнольдса в конце пористой поверхности находится из решения интегрального уравнения энергии
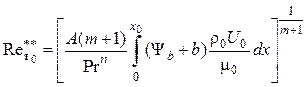 .
(5.12)
.
(5.12)
Тогда параметр эффективности завесы при вдуве через пористый участок будет
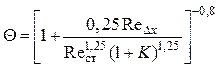 ,
(5.13)
,
(5.13)
где ![]() ,
, ![]() .
.
5.2. Теплообмен в области газовой завесы
с газовой завесой
на неадиабатической поверхности
Рассматриваемые условия соответствуют комбинированному способу охлаждения обтекаемой поверхности, когда наряду с локальной подачей охладителя непосредственно в пограничный слой происходит регенеративный теплообмен через стенку. Необходимо определить коэффициент теплоотдачи в области газовой завесы. Схемы завесы на адиабатической и неадиабатической поверхностях показаны на рис 5.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.