Теоретическая механика: Контрольные задания и указания к их выполнению по темам "Статика твердого тела", "Кинематика", "Динамика"

Определить натяжение Т троса, если радиус барабана, на который он намотан, равен r (м). Массой барабана крестовины и троса, а также трением пренебречь.

Таблица Д2.6

Номер условия	0	1	2	3	4	5	6	7	8	9
Р1	2	3	4	5	6	3	2	4	5	6
l	0.6	0.5	0.8	0.4	0.6	0.5	0.4	0.8	0.6	0.8
P2	8	10	12	14	16	15	18	20	10	16
r	0.1	0.2	0.3	0.1	0.4	0.3	0.1	0.3	0.4	0.2

К рис. Д2.7

Груз весом Р поднимается при помощи ворота. Вес барабана ворота Q(Н), радиус барабана r(м), длина рукоятки ОА=(м). Считая силу F приложенной перпендикулярно к рукоятке барабана, постоянной по величине, определить закон движения груза и натяжения Т троса, если в начальный момент скорость груза была равна нулю. Барабан считать однородным цилиндром. Массой рукоятки пренебречь.

Таблица Д2.7

Номер условия	0	1	2	3	4	5	6	7	8	9
Q	10	8	6	12	14	15	16	12	8	6
r	0,5	0,4	0,3	0,2	0,1	0,2	0,15	0,1	0,2	0,1
	1,0	1,2	1,5	1,6	0,8	0,6	0,5	1,0	1,2	0,5
F	5	6	7	8	9	10	12	14	15	26
P	2	3	4	5	6	7	8	9	10	12

К рис. Д2.8

Прямолинейная трубка АВ=(м) и весом Р₁(Н), наклоненная к вертикальной оси OZ под углом , вращается вокруг этой оси с угловой скоростью (рад/с) вместе с находящимся в ней шариком К весом Р₂(Н), привязанным нитью длиной а(м) в точке А. В некоторый момент нить обрывается. Определить угловую скорость вращения трубки в момент, когда шарик достигнет точки В, если момент инерции трубки относительно оси OZ равен J (кг м²).

Таблица Д2.8

Номер условия	0	1	2	3	4	5	6	7	8	9
a	90	45	30	60	90	60	90	30	45	30
J	3,72	3	1,92	3,84	2,56	6,08	3,4	1,5	2,19	3,36
	1,2	1	0,8	1,2	1,6	1,6	0,9	0,6	1,8	1,6
a	0,2	0,5	0,2	0,4	0,4	0,6	0,4	0,2	0,4	0,2
P2	7,25	9,8	4,9	2,45	2,45	9,8	4,9	2,45	4,9	9,8
wo	4	7	4,9	3	2	3	6	4	6	6

К рис. Д2.9

Винт судна имеет момент инерции J (кг м²) и приводится во вращение из состояния покоя вращающим моментом М (Нм). Винт испытываем момент сил сопротивления воды М_сопр.=к² (Нм). Определить угол поворота винта за промежуток времени, по истечении которого угловая скорость его станет равной ₁(рад/с).

Таблица Д2.9

Номер условия	0	1	2	3	4	5	6	7	8	9
J	50	55	60	65	70	75	80	85	90	100
М	40	50	60	70	80	90	100	120	150	160
К	2	3	4	5	6	7	8	3	2	4
1	10	15	20	25	30	35	40	45	50	60

ПРИМЕР

решения задачи типа Д2

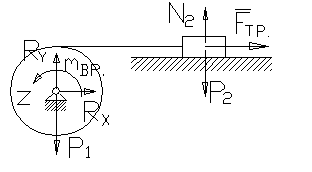            Под действием вращающего момента m_вр барабан весом Р₁ и радиусом r начинает вращаться вокруг неподвижной оси Z и на его боковую поверхность наматываемся нить, которая приводит в движение груз весом Р₂, скользящий по неподвижной горизонтальной плоскости, коэффициент трения которой .

Определить горизонтальную составляющую реакции неподвижной оси Z.

Применим теорему об изменении кинетического момента системы относительно оси Z (за механическую систему выберем барабан, нить и груз).

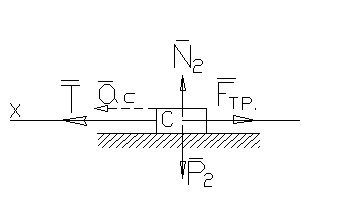
                                       (1)

Здесь внешними силами являются веса барабана и груза: Р₁, Р₂; реакция неподвижной оси Z: , реакция шероховатой поверхности: N₂ и F_тр=.

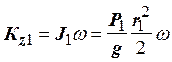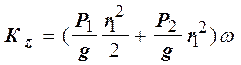; ; . Так что, . (2)

 (3). Учитывая (1), (2) и (3), получим:

.

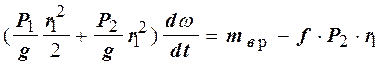Отсюда угловое ускорение барабана будет определяться так:

.

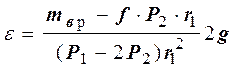Затем за механическую систему выберем груз и запишем для него теорему о движении центра масс в проекции на ось Х: . Отсюда  или, учитывая (3),

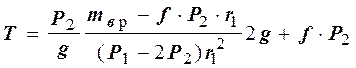 (4).

Задача Д3

Механическая система состоит из груза I (коэффициент трения скольжения груза о плоскость =0,1), невесомого шкива 2, цилиндрического однородного катка 4 радиусом м и ступенчатого шкива 3 с радиусами ступеней м, м и моментом инерции J (кг м²) (рис. Д3.0-Д3.9, табл. Д3). Тела системы соединены невесомыми нерастяжимыми нитями. Под действием постоянной силы (Н) система приходит в движение их состояния покоя. При движении системы на шкив 3 действуем постоянный момент сил сопротивления М_сопр. (Нм). Определить скорость груза 1 в момент времени, когда точка приложения силы  получит перемещение (м).

Таблица Д3

Номер условия	m3	m4	Mc	J3	F	S
0	2	10	0,1	0,2	100	1,0
1	3	9	0,2	0,4	120	1,2
2	4	8	0,3	0,3	140	1,4
3	5	7	0,2	0,5	150	1,6
4	6	6	0,1	0,6	120	1,8
5	7	5	0,3	0,2	160	2,0
6	8	4	0,2	0,4	180	1,5
7	9	2	0,1	0,3	200	1,6
8	10	3	0,3	0,2	210	1,8
9	6	8	0,2	0,5	150	2,0

Методические указания

Задача Д3 - на применение теоремы об изменении кинетической энергии системы (см. [I], стр. 369-383).

ПРИМЕР

решения задач типа Д3

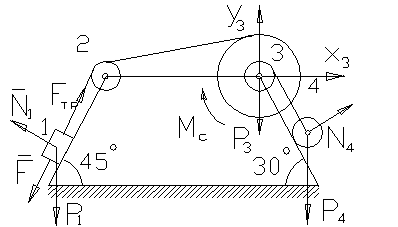
Механическая система состоит из груза 1 m₁=6 кг (коэффициент трения скольжения груза о плоскость=0,1), невесомого шкива 2, цилиндрического однородного катка 4 m₄=8 кг, радиуса м и ступенчатого шкива 3 с радиусами ступеней м, м и моментом инерции J₃=0,5 кгм². Тела системы соединены невесомыми нерастяжимыми нитями. Под действием постоянной силы F=150 Н система приходит в движение их состояния покоя. При движении системы на шкив 3 действует постоянный момент сил сопротивления М_с=0,2 Нм. Определить скорость груза 1 в момент времени, когда точка приложения силы F получит перемещение S₁=2,0 м.

Запишем теорему об изменении кинетической энергии механической системы в интегральной форме . Здесь имеем дело только с внешними силами, так как все тела системы твердые, а нити нерастяжимые. Подсчитаем сумму работ внешних сил:

 Нм; ;

Нм.

Нм.

, так как точка приложения сил неподвижна.

Нм.

.                 .

 м.       Поэтому Нм.

Нм

Вычислим теперь кинетическую энергию системы:  (так как система покоилась). . ; ; ; ; ; ; ; ; ; .

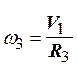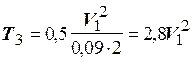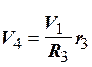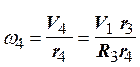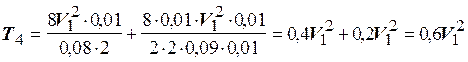Подставляя найденные значения  и , получим

; м/с.

Задача Д4

Вертикальный вал АК (рис. Д4.0 - Д4.9, табл. Д4), вращающийся с постоянной угловой скоростью =10 рад/с, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д4, в столбце 2 (АВ=ВД=ДЕ=ЕК=а). К валу жестко прикреплены невесомый стержень 2 длиной м с точечной массой  кг на конце и невесомый стержень 2 с длиной м с точечной массой кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице, в столбцах 3 и 4, а углы a и b - в столбцах 5 и 6; пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять а= 0,4м.

Таблица Д4

Номер	Подшипник	Крепление
условия	в точке	стержня 1 в точке	стержня 2 в точке	ao	bo
0	В	К	Д	30	45
1	Д	Е	В	45	60
2	Е	В	Д	60	30
3	К	Е	Д	90	60
4	В	Д	Е	30	90
5	Д	К	В	30	60
6	Е	В	К	45	30
7	К	Е	В	60	30
8	Д	Е	Е	90	30
9	Е	К	Д	30	60

Методические указания

Задача Д4 - на применение к изучению системы принципа Даламбера