Максимум функции, дифференциал второго порядка и экстренум - вопросы

Лекция 1

1.  Какое максимальное приращение аргумента возможно для функции y=arcsin(x) в точке x=0, и какое ему будет соответствовать приращение функции?

2.  Какой из рассмотренных производных нужно воспользоваться, чтобы найти производную функции, график которой изображен на рисунке

 

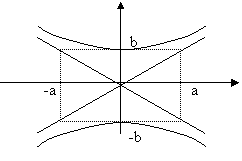Записать уравнение этой функции.

3.  Пользуясь производной сложной функции запишите, чему равна производная функции

y(u)=f(g(x(t(u))))

4.  В какой точке мгновенная скорость движения, описываемого графиком больше, почему?

5.  На каком промежутке можно найти y’_x для функции y=ln(t), x=1/(t+1)?

Лекция 2

1.  В выводе формулы для дифференциала второго порядка обосновать переход

.

2.  Сформулировать геометрический смысл дифференциала.

3.  Пояснить, почему в формуле Лагранжа .

4.  Привести геометрическую иллюстрацию функции, для которой выполнены условия теоремы Лагранжа и точек  несколько.

5.  Приближенно вычислить  с помощью дифференциала (любым произвольным способом).

6.  Записать разложение по формуле Маклорена функции .

Лекция 5

1.  Привести пример функции, заданной аналитически, которая имеет точку экстремума и в этой точке не существует производная функции.

2.  Привести пример функции, заданной аналитически, которая имеет вертикальную асимптоту.

3.  Привести пример функции, заданной аналитически, график которой симметричен

а) относительно оси OY,

б) относительно точки О(0,0).

4.  По данному графику функции  построить примерный график ее первой производной.

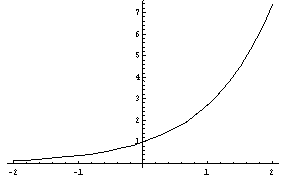
5.  Исследовать функцию  на экстремум с помощью производных высших порядков.