Задача 1
В магазин поступило $(a) цифровых фотоаппаратов, среди которых $(b) имеют дефекты. Наудачу отбирается 1 фотоаппарат. Какова вероятность того, что он не имеет скрытых дефектов?
Отв (a-b)/a
Задача 2
В урне содержится $(a+b+c) шаров , среди которых $(a) белых, $(b) синих, $(c) красных. Наудачу отбираются $(m) шаров и откладываются. Найти вероятность того, что все отложенные шары белые.
Отв 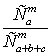
Задача 3
Стрелок производит выстрел по мишени квадратной формы, сторона которой равна $(a) см. Найти вероятность того, что место поражения отклонится от центра мишени не более чем на $(b) см.
Отв ![]()
Задача 4
Вероятность того, что локальная сеть будет бесперебойно функционировать с 8 до 12 часов равна 0,$(a), а вероятность того, что она будет бесперебойно функционировать с 8 до 20 часов равна 0,$(a-2). Какова вероятность того, что сеть, бесперебойно проработавшая до 12 часов, проработает и до 20 часов?
1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.