Введем функцию 6i/(p)=y^—y/y, определяющую меру сбалансированности спроса и предложения. Ее называют избыточным спросом. Она может быть положительной и отрицательной; во втором случае фактически имеется излишек товара. Предположим, что регулирование цены происходит без запаздывания и 6у(р) непрерывна, монотонна и на интервале p's^p^p" имеет один положительный корень р.
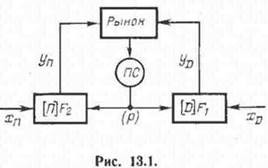
На рис. 13.1 показана схема регулирования цены, в которой отрицательная обратная связь (см. 2.3) изображена в виде некоторого посредника <ПС», вычисляющего общий избыточный спрос на рынке и сообщающего соответствующую информацию его участникам.
Предположим, процесс регулирования реализуетсятак, что
![]()
т. е. скорость изменения цены пропорциональна избыточному спросу. Такое предположение является достаточно естественным и существенно упрощает решение задачи регулирования. Пусть далее спрос и предложение—линейные функции цены:
![]()
и координаты точки А (см. рис. 13.2) определяют се равновесную величину:
![]()
Допустим, что при t=0 возник избыточный спрос и цена отклонилась от ее равновесного значения на 6р(0), определяемую из (13.3). Тогда регулирование будет осуществляться в соответствии с дифференциальным уравнением (13.2), которое примет вид
![]()
откуда при указанных выше начальных условиях найдем
![]()
Обычно Оо<0; Ро>0. Если |Ро[>1с(о| (прямая спроса ДДкручепрямой предложения ПП), то у<0 и при t—*oo бр—"0.
При запаздывании спроса и предложения на изменение цены процесс рыночного регулирования приобретает колебательный характер. Размах колебаний и время достижения равновесия (если оно достижимо) зависят от соотношения величин а, р, р^ и р*.
Условия устойчивости рынка. Рынок называют устойчивым, если при любых начальных ценах р(0) величина p(f) приближается к равновесию.
Проблеме устойчивости рынка посвящены многие работы известных представителей буржуазной политэкономии и эконометрии (Л. Вальрас, В. Парето, Дж. Хикс, П. Самуэльсрн, К. Эрроу и др.). Экономика обычно рассматривается в них как множество отдельных производителей и потребителей, и рассматриваемая ими модель системы общего равновесия замкнута в том смысле, что вся совокупность переменных определяется заданными условиями. Чтобы убедиться в совместимости системы с состоянием равновесия, необходимо сопоставить число уравнений с числом неизвестных. Однако нам ничего не известно ни о существовании, ни о единственности состояния равновесия. Мы не получаем также, никакого указания относительно динамической устойчивости равновесия. Помимо слабости формальных предпосылок, как показал венгерский экономист Я. Корнай, теория и модели общего рыночного равновесия абстрагируются от важнейших реальных условий современной капиталистической экономики: концентрации капитала, роли монополий, государственного вмешательства, неценовой информации и ряда других внерыночных факторов.
Приведем модель общего равновесия в упрощенном виде. Ее переменные—количества проданных или купленных производителями и потребителями товаров. Пусть нижний индекс qiq^l, т) соответствует видам товаров, а индекс i (1=\, п) — индивидуумам, совершающим покупки-продажи. Так, например, i/g i — интенсивность покупки (продажи) товара q индивидуумом i. Обозначим цену, по которой обменивается товар q через рд. Поскольку достаточно определить лишь соотношения для цен, примем цену товара т равной единице: /?т=1. Тогда общее число переменных в модели, описывающей процесс обмена, определится так; тп переменных
yqi плюс т—\ переменных для цен pq. Следовательно, всего [т(п+1)—1] переменных.
Следуя Р. Аллену, примем, что существуют две группы условий рыночного равновесия.
1. Как и в (5.22). принимается, что для каждого индивидуума (' существует некоторая функция от всего набора товаров
![]()
с непрерывными частными производными, которую он стремится максимизировать при условии сбалансированности своего бюджета:
![]()
Здесь у~{ —объем товара q, первоначально имевшегося у индивидуума (. Условный экстремум и, определяется из соотношения
![]()
где у—множитель Лагранжа. Полагая далее входящие в набор товары взаимозаменяемыми, найдем, что предельные нормы замещения (см. также (5.26)) при рт -с 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.