Производная функции. Задачи, приводящие к понятию производной. Связь между непрерывностью и дифференцируемостью функции

Производная функции

Тема: Производная функции 1. Задачи, приводящие к понятию производной. 1.1. Скорость прямолинейного движения 1.2. Касательная к кривой 2. Определение производной; ее механический и геометрический смысл. Уравнение касательной и нормали к кривой 3. Связь между непрерывностью и дифференцируемостью функции 4. Производная суммы, разности, произведения и частного 5. Производная сложной и обратной функции

6. Производные основных элементарных функций 6.1. Степенная функция 6.2. Показательная функция 6.3. Логарифмическая функция 6.4. Тригонометрические функции 6.5. Обратные тригонометрические функции 7. Гиперболические функции и их производные 8. Таблица производных 8.1. Правила дифференцирования 8.2. Формулы дифференцирования

1.Задачи, приводящие к понятию производной

Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.

1.1.Скорость прямолинейного движения

Пусть материальная точка (некоторое тело) М движется неравномерно по некоторой прямой. Каждому значению времени t соответствует определенное расстояние ОМ = S до некоторой фиксированной точки О. Это расстояние зависит от истекшего времени t , т. е. S= S(t)

M

О

M1

l

Рис. 1.

S (t)

S (t + t)

Это равенство называют законом движения точки. Требуется найти скорость движения точки.

Если в некоторый момент времени t точка занимает положение М, то в момент времени

- приращение времени) точка займет положение M , где ОМ = S + S

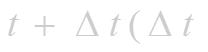
( S – приращение расстояния) (см. рис. 1), Таким образом, перемещение точки М за время

t будет

S = S(t +

t) - S(t)

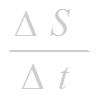
Отношение выражает среднюю скорость движения точки за время :

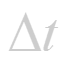
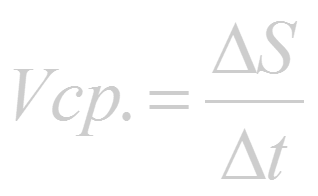
Средняя скорость зависит от значения t: тем меньше t, тем точнее средняя скорость выражает скорость движения точки в данный момент времени t.

Предел средней скорости движения при стремлении к нулю промежутка времени t называют скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив эту скорость через V, получим

или

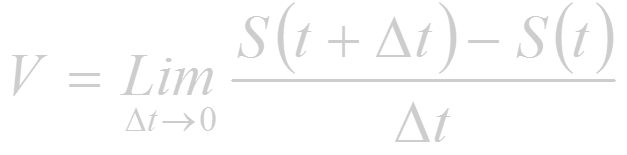
(1.1)

1.2. Касательная к кривой

Дадим сначала общее определение касательной к кривой. Возьмем на непрерывной кривой L две точки М и М1 (см. рис. 1.2.). Прямую М М1, проходящую через эти точки, называют секущей. Пусть точка М1, двигаясь вдоль кривой L, неограниченно приближается к точке M. Тогда секущая, поворачиваясь около точки M, стремится к некоторому предельному положению MT.

Касательной к данной кривой в данной точке М называется предельное положение МТ секущей М М1, проходящей через точку М, когда вторая точка пересечения М1 неограниченно приближается по кривой к точке M1.

T

M1

L

M

Рис. 1.2.

y

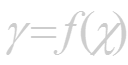
M1

T

M

y

x

O

Рис.1.3.

Рассмотрим теперь график непрерывной кривой имеющий точке М невертикальную касательную. Найдем ее угловой коэффициент , где - угол касательной с осью Ох.

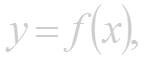
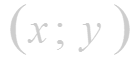
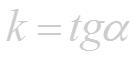
Для этого проведем через точку М1 и точку М графика с абсциссой . секущую (см. рис. 1.3.). Обозначим через - угол между секущей М М1 и осью Оx. На рисунке видно, что угловой коэффициент секущей равен

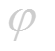
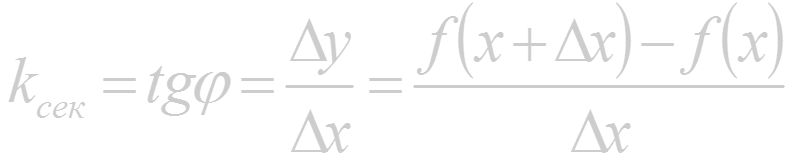
При в силу непрерывности функции приращение тоже стремится к нулю; поэтому точка М1 неограниченно приближается по кривой к точке М, а секущая М М1, поворачиваясь около точки М, переходит в касательную. Угол , т.е

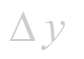
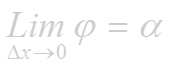
Следовательно,

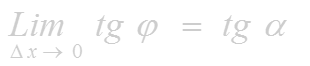
Поэтому угловой коэффициент касательной равен (1.2)

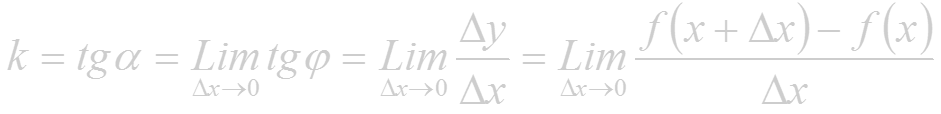
К нахождению пределов вида (1.1) и (1.2) приводит решения и множества других задач. Можно показать, что:

- если Q = Q(t) - количество электричества, проходящего через поперечное сечение проводника за время t, то сила тока в момент времени t равна

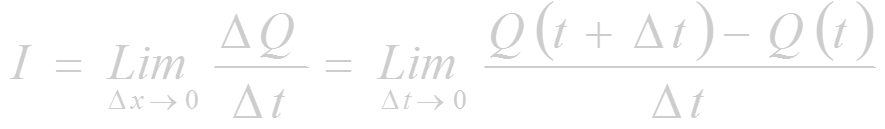
(1.3)

- если N = N(t) - количество вещества, вступающего в химическую реакцию за время t, то скорость химической реакции в момент времени t равна

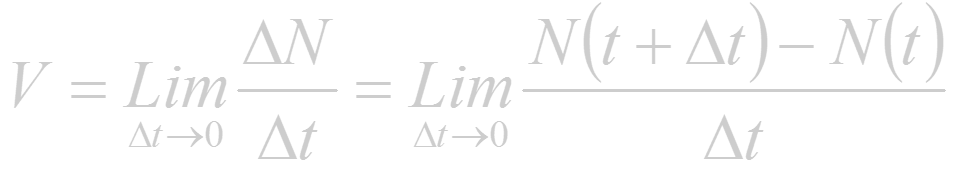
(1.4)

- если m=m(x)- масса неоднородного стержня между точками O(0:0) и М(х;0), то линейная плотность стержня в точке x есть

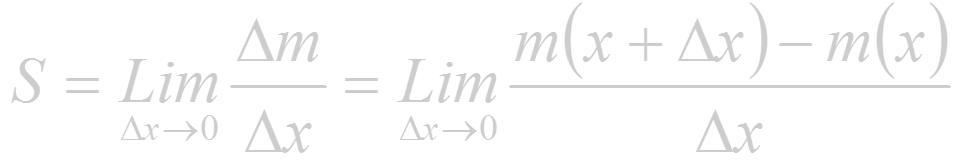
(1.5)

Пределы (1.1)-(1.5) имеют одинаковый вид; везде; требуется найти предел отношения приращения функции к приращению аргумента. Этот предел называют производной. Эти пределы можно записать так:

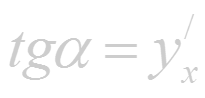
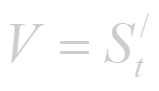
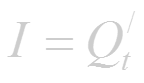
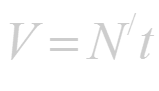
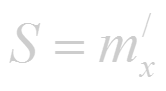
(читается «V равно S штрих по t », « тангенс у равен у штрих по x » и т.д.).

2.Определение производной; ее механический и геометрический смысл. Уравнение касательной и нормали к кривой

Пусть функция определена на некотором интервале (а; b). Проделаем следующие операции:

- аргументу (а;b) дадим приращение

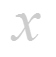
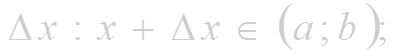
- найдем соответствующее приращение функции:

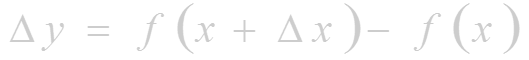
- составим отношение приращения функции к приращению аргумента:

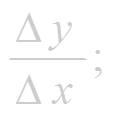
-найдем предел этого отношения при

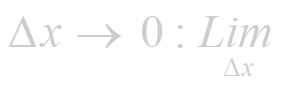
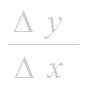
Если этот предел существует, то его называют производной функции и обозначают одним из символов

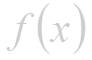
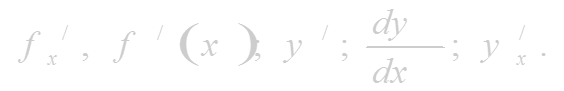
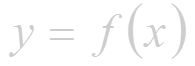
Производной функцuu в точке называется предел приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

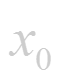
Итак, по определению

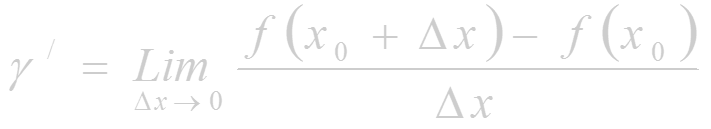
или

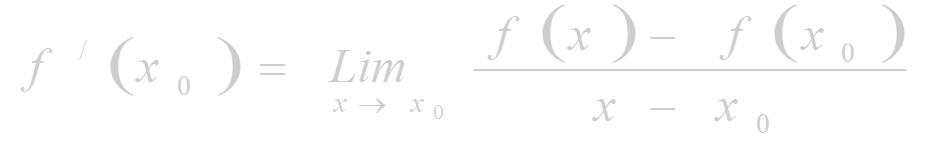
Производная функции есть некоторая функция , произведенная из данной функции.

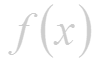
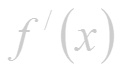
Функция , имеющая производную в каждой точке интервала (а; b), называется дuфференцuруемой в этом интервале; операция нахождения производной