Числовые множества. Множества действительных чисел. Числовые промежутки. Окрестность точки

МНОЖЕСТВА

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

План:

1. Основные понятия.
2. Числовые множества. Множества действительных чисел.
3. Числовые промежутки. Окрестность точки.

1. Основные понятия.

Понятие множества является: одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединённых по какому-либо признаку. Так можно говорить о множестве студентов института, о множестве рыб в Черном море, о множестве корней уравнения х2 + 2х + 2 = 0, о множестве всех натуральных чисел и т. д.

Объекты, из которых состоит множество, называются, его элементами. Множества принято обозначать заглавными буквами латинского алфавита А, В, ...,Х,Y,.., а их элементы — малыми буквами а,Ь,...,x,y,… Если элемент х принадлежит множеству X, то записывают х X; запись х X или х X означает, что элемент х не принадлежит множеству X. Множество, не содержащее ни одного элемента, называется пустым, обозначается символом .

Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества. Например, запись А={1,3,15} означает, что множество А состоит из трех чисел 1, 3 и 15; запись А = { х : 0 х 2} означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0 х 2.

Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В. Символически это обозначают так А В («А включено в В») или В А («множество В включает в себя множество А»). Говорят, что множества А и В равны или совпадают, и пишут А=В, если А В и В А. Другими словами, множества, состоящие из одних и тех же элементов называются равными.

Объединением (или суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают А В (или А + В). Кратко можно записать А В = {х : х А или х В}.

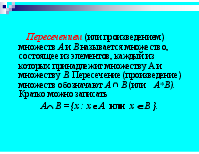
Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают А В (или А*В). Кратко можно записать А В = {х : х А или х В }.

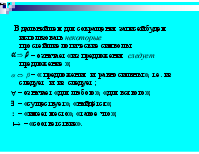
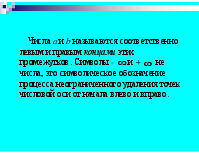
В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы: – означает «из предложения следует предложение »; – « предложения и равносильны », т.е. из следует и из следует ; – означает «для любого», «для всякого»; – «существует», «найдётся»; : – «имеет место», «такое что»; – «соответствие».

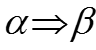
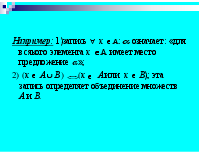
Например: 1)запись х : означает: «для всякого элемента х имеет место предложение »; 2) (х А В ) (х А или х В); эта запись определяет объединение множеств А и В.

2. Числовые множества. Множества действительных чисел

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются: N = {1; 2; 3; …; n; …} – множество натуральных чисел; Z0 = {0; 1; 2; …; n; …} – множество целых ненатуральных чисел; Z = {0; 1; 2; …; n; …} – множество целых чисел; Q = { : m Z, n N} – множество рациональных чисел; R – множество действительных чисел. Между этими множителями существует соотношение N Z0 Z Q R.

Множество R содержит рациональное и иррациональное числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, = 0,5 (= 0,500…), = 0,333… –рациональные числа. Действительные числа, не являющиеся рациональными, называются иррациональными.

• Теорема. Не существует рационального числа,
• квадрат которого равен числу 2.

Допустим, что существует рациональное число, представленное несократимой дробью , квадрат которого равен 2. Тогда имеем: = 2, т.е. m2 = 2n2.

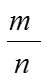
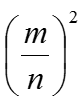
Отсюда следует, что m2 (а значит, и т) – четное число, т.е. т = 2k. Подставив т = 2k в равенство m2 = 2n2, получим 4k 2 = 2n2, т.е. 2k 2 = n2. Отсюда следует, что число n – четное, т.е. n = 2l. Но тогда дробь = сократима. Это противоречит допущению, что дробь несократима. Следовательно, не существует рационального числа, квадрат которого равен числу 2.

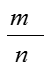
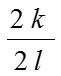
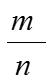
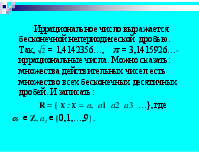
Иррациональное число выражается бесконечной непериодической дробью. Так, = 1,4142356…, = 3,1415926…-иррациональные числа. Можно сказать: множества действительных чисел есть множество всех