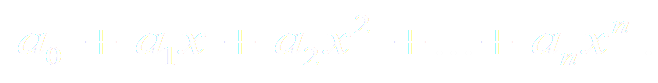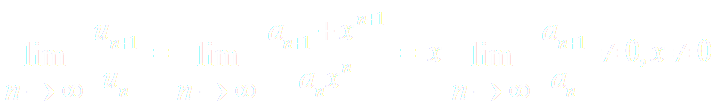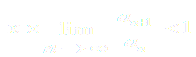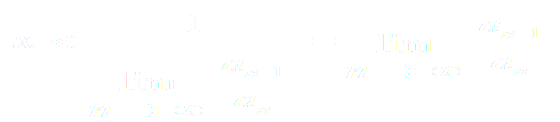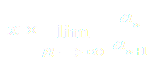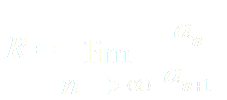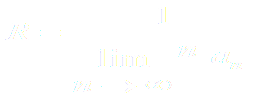Степенные ряды. Функциональные ряды. Основные понятия

Тема:

СТЕПЕННЫЕ РЯДЫ

План лекции

• Функциональные ряды
• Основные понятия

ОСНОВНЫЕ ПОНЯТИЯ

• Ряд, членами которого являются функции от x, называется функциональным:

• (1)

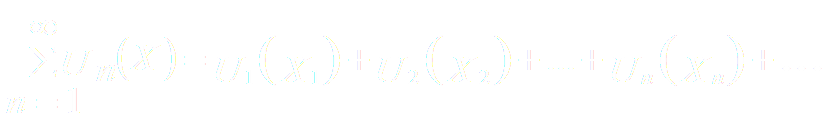
• Придавая x определённое значение x0, мы получим числовой ряд

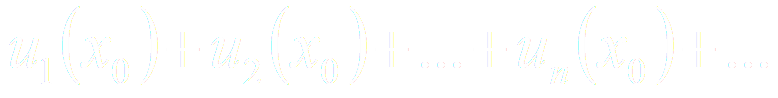
• который может быть как сходящимся, так и расходящимся.

• Если полученный числовой ряд сходится, то точка x0 называется точкой сходимости ряда (1); если же ряд расходится – точкой расходимости функционального ряда.

• Совокупность числовых значений аргумента x, при которых функциональный ряд сходится, называется его областью сходимости.

• В области сходимости функционального ряда его сумма является некоторой функцией от x: S=S(x). Определяется она в области сходимости равенством.

• Частичная сумма ряда

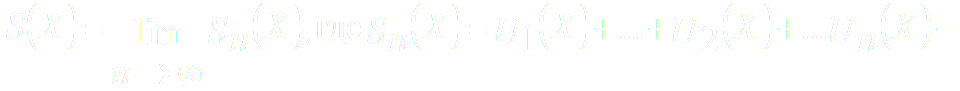
ПРИМЕР 1. Найти область сходимости ряда

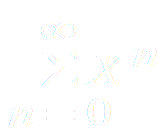
• Решение: Данный ряд является рядом геометрической прогрессии со знаменателем q=x. Следовательно, этот ряд сходится при ׀x׀ < 1 т.е при всех x Є (-1;1) сумма ряда равна :

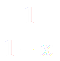
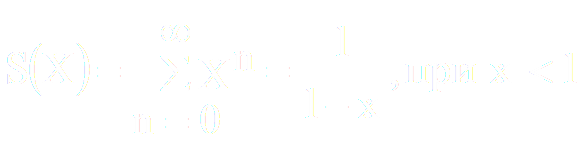
ПРИМЕР 2. Исследовать сходимость функционального ряда

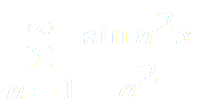
• Решение: Составим ряд из абсолютных величин членов исходного ряда:

• (2)

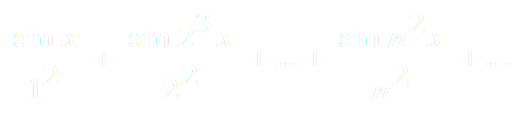
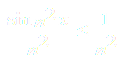
• Так как при любом X Є R имеет место соотношение а ряд с общим членом сходится (обобщённый гармонический ряд), то по признаку сравнения ряд (2) сходится при X Є R. Следовательно, исходный ряд абсолютно сходится при всех X Є R =(-∞;+∞).

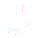
• Среди функциональных рядов в математике и ее приложениях особую роль играет ряд, членами которого являются степенные функции аргумента x, т.е так называемый степенной ряд.

• (3)

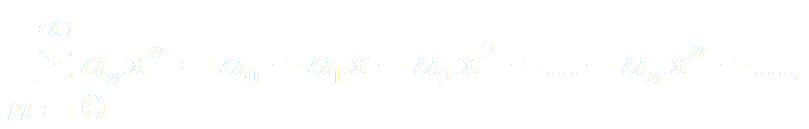
• Действительные (или комплексные) числа a0, a1, a2, …, an ,… .называются коэффициентами ряда (3), X Є R – действительная переменная.

• Ряд (3) расположен по степеням x. Рассматривают также степенной ряд, расположенный по степеням (X – X0), т.е ряд вида

• (4)

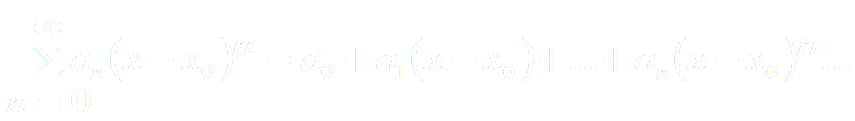
• Где x0 – некоторое постоянное число.

• Ряд (4) легко приводится к виду (3), если положить x – x0 = z. Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (3)

ТЕМА:

СХОДИМОСТЬ СТЕПЕННЫХ РЯДОВ

План лекции:

• Теорема Н. Абеля
• Интервал и радиус сходимости степенного ряда
• Свойства степенных рядов

Теорема Н. Абеля

Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.

• Теорема 1 (Абель). Если степенной ряд (3) сходится при X = X0 ≠ 0, то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству ׀x׀<׀x0׀.

• По условию ряд сходится. Следовательно, по необходимому признаку сходимости .Отсюда следует, что величина oграничена, т.е найдётся такое число М > 0, что для всех n выполняется неравенство

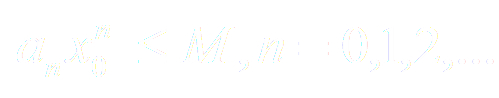
• Пусть ׀x׀<׀x0׀, тогда величина и, следовательно,

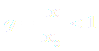
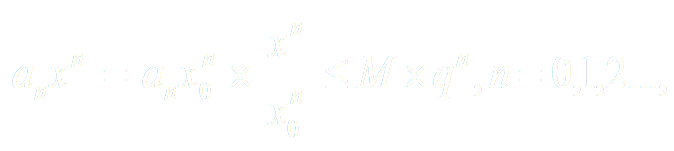
т.е модуль каждого члена ряда(3) не превосходит соответствующего члена сходящегося (q < 1) ряда геометрической прогрессии. Поэтому по признаку сравнения при ׀x׀<׀x0׀ ряд (3) абсолютно сходящийся.

Следствие 1. Если ряд (3) расходится при x = x1, то он расходится и при всех х, удовлетворяющих неравенству ׀x׀>׀x1׀

• Действительно, если допустить сходимость ряда в точке х2, для которой ׀x2׀>׀x1׀, то по теореме Абеля ряд сходится при всех х, для которых ׀x׀<׀x2׀, и, в частности, в точке х1, что противоречит условию.

Интервал и радиус сходимости степенного ряда

• Из теоремы Абеля следует, что если х0 ≠ 0 есть точка сходимости степенного ряда, то интервал весь состоит из точек сходимости данного ряда; при всех значениях x вне этого интервала ряд (3) расходится.

Рис. 1

-R ряд сходится R ряд сходится О ряд расходится

• Интервал и называют интервалом сходимости степенного ряда. Положив ,интервал сходимости можно записать в виде(-R;R). Число R называют радиусом сходимости степенного ряда, т.е R > 0 – это такое число, что при всех x, для которых ,ряд (3) абсолютно сходится, а при ряд расходится.

• В частности, когда ряд (3) сходится лишь в одной точке х0 = 0, то считаем, что R = 0. Если же ряд (3) сходится при всех значениях x Є R (т.е во всех точках числовой оси ), то считаем, что R = ∞.

Отметим, что на концах интервала сходимость (т.е при x = R и при x = - R) сходимость ряда проверяется в каждом случае отдельно.

Для нахождения радиуса сходимости степенного ряда (3) можно поступить следующим образом.

Составим ряд из модулей членов данного степенного ряда

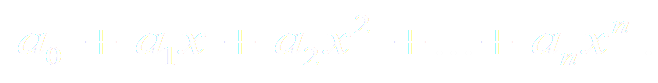
• и применим к нему признак Даламбера. Допустим, что существует предел

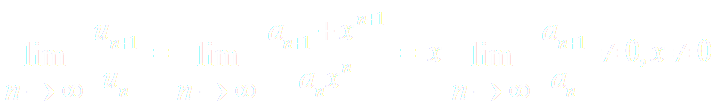
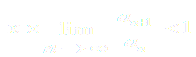
По признаку Даламбера ряд сходится, если т.е ряд сходится при тех значениях x, для которых

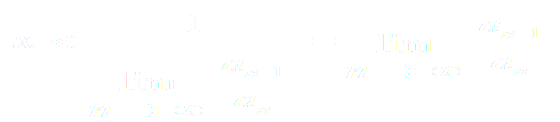
• ряд, составленный из модулей членов ряда (3), расходится при тех значениях х, для которых

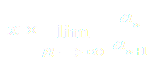
• Таким образом, для ряда (3) радиус абсолютной сходимости

(1)

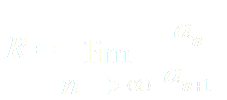
• Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что

(2)

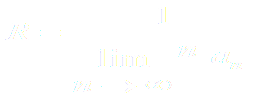
Замечания

• 1. Если , то можно убедиться, что ряд (4) абсолютно сходится на всей
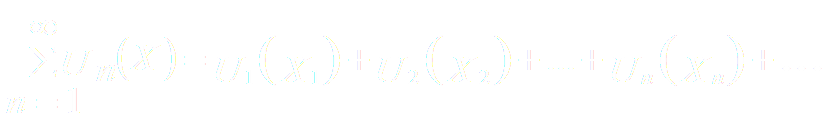
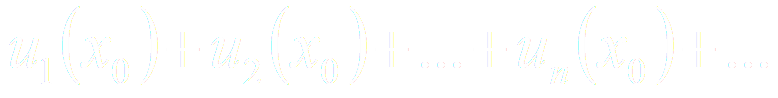
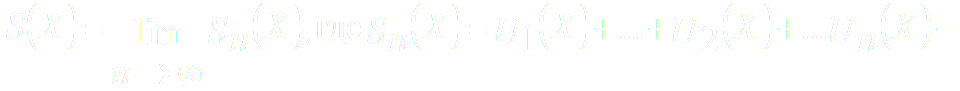
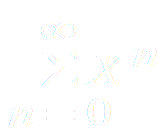
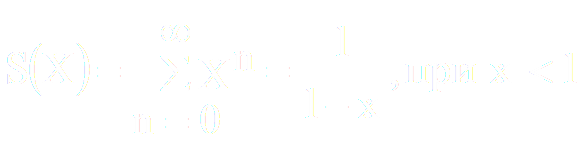
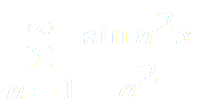
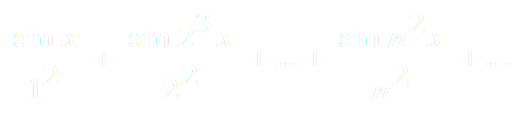
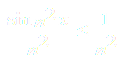
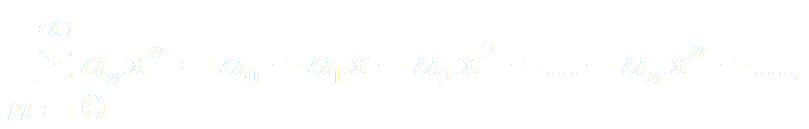
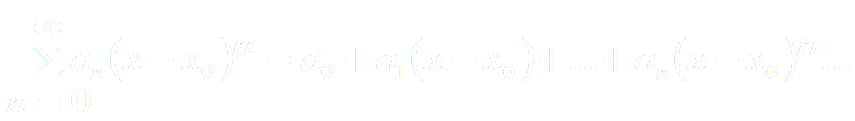
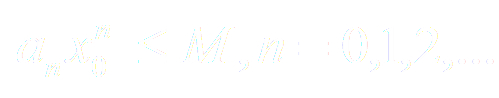
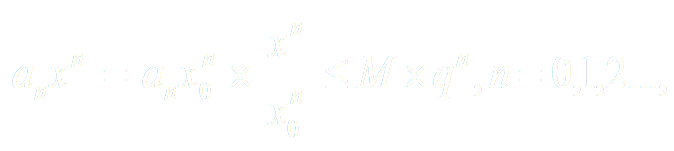