Разработка индивидуального привода (мощность выходного вала привода - 1800 Вт), страница 2

σ _Нlimb = 2∙265+70=600МПа.

Базовое число циклов перемены напряжений по графику (рис. 6.21.ч.1[1]:

N_HО =17,5∙10⁶=1,75∙10⁷циклов (НВ265).

Коэффициент долговечности:

К_NL=.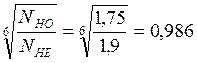

Примем коэффициент безопасности S_H=1,1. тогда допускаемое напряжение:

σ _HP=(σ _Hlimb/ S_H)∙К_NL=(600/1,1)∙0,986=538 МПа.

Изгибные напряжения. По табл. 6.16 4.1[1] примем σ_Flimb=260+HB. При  среднем значении твердости после улучшения НВ265 получим: σ_Flimb=260+265=525 МПа.

Коэффициент безопасности S_F=1,7. поскольку нагрузка односторонняя примем К_FC=1 (стр.134 ч.1[1]).

          Рекомендуется принимать для всех сталей N_FО=4∙10⁶, тогда коэффициент долговечности:

К_FL==.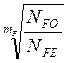

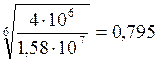Допускаемое напряжение:

σ_FP = (σ _Flimb/ S_F)∙К_FL∙К_FC=(525/1,7)∙0,795∙1=245МПа.

Определяем размеры передачи и колес.

Ориентировочное значение среднего модуля для прямозубых колес определяется по формуле 6.27. ч.1[1]

m_m=14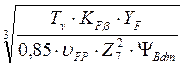 , где T_v- момент на ведущем валу;

T_v=313,8 Н∙м.

К_ве=, где=0,6, U=2 (передаточное число) ст.126 ч.1[1], значит,

К_ве=.

Принимаем исходя из этого К_ве=0,35. К_Fβ- коэффициент, учитывающий неравномерное распределение нагрузки по ширине венца. Выбирается в зависимости от величины (К_ве∙U)/(2∙К_ве)=(0,35∙2)/(2-0,35) = 0,424 по рис. 6.19 ч. 1[1]:    К_Fβ=1,3 и К_Нβ=1,14.

Y_F принимаем по графику (рис. 6.14.ч.1[1]):Y_F=3,895.

 

, где δ₁- угол делительного конуса шестерни и tgδ₁=1/4=0,5;  δ₁=26,56°

,тогда:

m_m=14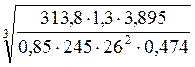=4,028.

По расчетному модулю для прямозубых колес вычисляется модуль:

m_e=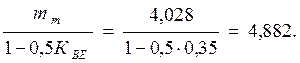

По СТСЭВ310-76 ст.110 ч.1[1] принимаем модуль: m_e=5.

Затем вычислим параметры колес передачи по формулам табл. 6. 2. ч.1[1]:

Средний окружной модуль: m_m= 4

Внешний окружной модуль: m_е= 5

Углы делительных конусов: δ₁=26,6;  δ₂=90-δ₁=63,4°

Внешнее конусное расстояние: R_е=0,5 m_е=145мм.

Ширина зубчатого венца: b_ωК_ве∙ R_е    b_ω51                                              b_ω10m_e       b_ω50   b_ω=50мм

Среднее конусное расстояние: R_m=R_e-0,5∙ b_ω=120мм

Внешний делительный диаметр: d_e7= m_еZ₇=5∙26=130мм

d_e8=5∙52=260мм

Средний делительный диаметр: d_m7=(1-0,5K_be)∙ d_e7=107 мм ;

d_m8=(1-0,5K_be)∙ d_e8=214 мм.

Параметры изображения зубчатой пары (z₇-z₈): см. рис.6.27.8) ч.1[1]

z₇                                                                         z₈

d_e==130 мм                                       d_e==260 мм                                   

d_{ступица}=1,6∙d_m                                                       d_{ступица}=100,8 мм

=54 мм                                         =75,6 мм

Проверочный расчет на выносливость по контактным напряжениям. Для прямозубых передач:   

σ _H=z_н∙z_м∙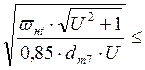σ_нр (6.22. ч.1[1])

для стальных колес z_м= 275 (МПа)

β_m ≈0, т.к. шестерня прямозубая,  z_н=cos β_m.

Удельная расчетная окружная сила:

ω_нt=∙К_нα∙ К_нβ∙ К_нδ= К_нα∙ К_нβ∙ ∙К_нδ    (6.24) ч.1[1]

К_нα=1 (для прямозубых), К_нβ=1,14 (рис. 6.19.ч.1.[1]).

Коэффициент, учитывающий динамическую нагрузку:

К_нδ=1+ (6.25); ω_Hδ= δ _н∙ q_о∙ δ _m∙; [Н/мм]

ω_Hδ- удельная окружная динамическая сила.

δ _m=0,004(табл.610 ч1[1])

q_о=82 (табл. 6.11.ч.1[1]), тогда:

ω_Hδ=0,006∙82∙0,33∙  , Н/мм

ω_Htp=-удельная расчетная окружная сила в зоне наибольшей концентрации. [Н/мм]

F_Ht=Н.

ω_Htp=Н/мм.

К_нδ=1+;   ω_Ht= Н/мм

σ_н=1∙275∙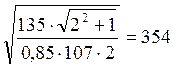МПа

Условие прочности выполняется:

354 МПа= σ_н< σ_нр=538 МПа.

Проверочный расчет на выносливость по напряжениям изгиба.

Требование усталостного излома гарантируется при выполнении условия:

σ_F=Y_F∙ σ_Fp (ст.129 ч.1[1]), где m_m=4; Y_F –коэффициент, учитывающий форму зуба

Y_F=3,895 ( по графику рис. 6.14.ч.1[1]);

ω_Ft=- удельная расчетная окружная сила.

F_Ft=H.

K_Fα=, где n - степень точности по нормам контакта (n=9)

=1,88-3,2(1/Z₇+1/Z₈)=1,88-3,2(1/26+1/52)=1,7

- коэффициент торцевого перекрытия.

K_Fα=; K_Fδ=1+, где ω_Ftp=(F_Ft/b_ω)∙K_Fβ=(5865/50)∙1,3=152,5 Н/мм

ω_Fδ=δ_F∙ q_о∙ δ_m∙=0,006∙82∙0,33=2,057 Н/мм

K_Fδ=1+=1,01.

ω_Ft==154,01 Н/мм

σ_F=3,895∙МПа;

условие прочности соблюдается:177МПа= σ_F < σ_FР =245МПа.

Параметры других передач:

а) пара прямозубых цилиндрических колес 1-2:

делительное межосевое расстояние:  α=К_α(U₁₂+1)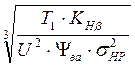

U=Z₂/Z₁=38/19=2; К_α=495(МПа);    K_Hδ=1,14;       

Т_I=8,12Н∙м

. 

Тогда  :  α=495(2+1)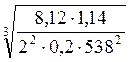=51 мм.

Модуль:   m=2α/Z_å=2∙51/(38+19)=1,79

Принимаем модуль: m=2мм

Уточняем межосевое расстояние:a=m_Zå/2=57мм

1-е колесо (шестерня):                                                       2-е колесо:

d_z1=m_z1=38мм                                                                      d_z2=76,7мм

b_ω=y_вa∙a=0,2∙57=11,4мм.

Геометрические параметры взяты по табл. стр.136 ч.1[1].

б) пара прямозубых цилиндрических колес 3-4:

аналогично пункту а): α=495(2,5+1)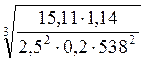=63 мм.