|
Таблица 4. |
||||||||||
|
|
|
|
|
Относительные частоты |
Абсолютные частоты |
|||||
|
|
|
|
|
|||||||
|
228 |
-50 |
-1,80 |
0,08 |
2,95 |
8,18 |
3,25 |
9,00 |
|||
|
238 |
-40 |
-1,44 |
0,14 |
5,27 |
6,36 |
5,80 |
7,00 |
|||
|
249 |
-29 |
-1,04 |
0,23 |
8,61 |
5,45 |
9,47 |
6,00 |
|||
|
259 |
-19 |
-0,68 |
0,32 |
11,73 |
15,45 |
12,90 |
17,00 |
|||
|
269 |
-9 |
-0,32 |
0,38 |
14,04 |
9,09 |
15,44 |
10,00 |
|||
|
280 |
2 |
0,08 |
0,40 |
14,74 |
10,91 |
16,21 |
12,00 |
|||
|
290 |
12 |
0,43 |
0,36 |
13,45 |
10,91 |
14,79 |
12,00 |
|||
|
300 |
22 |
0,79 |
0,29 |
10,78 |
14,55 |
11,86 |
16,00 |
|||
|
311 |
33 |
1,19 |
0,20 |
7,28 |
10,00 |
8,01 |
11,00 |
|||
|
321 |
43 |
1,55 |
0,12 |
4,45 |
9,09 |
4,89 |
10,00 |
|||
|
Сумма: |
93,29 |
100,00 |
102,61 |
110,00 |
||||||
|
Таблица 5. |
||||
|
|
|
|
|
|
|
9 |
3,25 |
5,75 |
33,0625 |
10,17307692 |
|
7 |
5,8 |
1,2 |
1,44 |
0,248275862 |
|
6 |
9,47 |
-3,47 |
12,0409 |
1,271478353 |
|
17 |
12,9 |
4,1 |
16,81 |
1,303100775 |
|
10 |
15,44 |
-5,44 |
29,5936 |
1,916683938 |
|
12 |
16,21 |
-4,21 |
17,7241 |
1,093405305 |
|
12 |
14,79 |
-2,79 |
7,7841 |
0,526308316 |
|
16 |
11,86 |
4,14 |
17,1396 |
1,445160202 |
|
11 |
8,01 |
2,99 |
8,9401 |
1,116117353 |
|
10 |
4,89 |
5,11 |
26,1121 |
5,339897751 |
|
Сумма: |
110 |
24,434 |
||
c2набл = 24,43 > c2теор = 14,1, следовательно, выборка не подчиняется нормальному закону распределения.
4. Переход к интегральному закону распределения
Перейдем к интегральной функции распределения и попытаемся найти ее значение путем разложения в ряд Грамм-Шарлье при нормированном отклонении Z = 2.
![]()
при Z = 2: ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
5. Определение доверительных интервалов
Учитывая, что отклонение от нормального закона распределения не велико, найдем доверительный интервал из предположения, что выборка подчиняется нормальному закону распределения.
![]() ,
, ![]() .
.
где ![]() ,
, ![]()
![]()
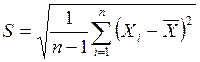 ;
;
k = 110 – 1 = 109; P=0,95; t = 1,96; zн=0,879; zв=1,16.
![]() ,
, 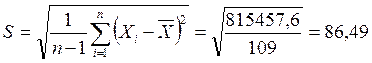 .
.
174,59< a < 206,92.
6. Сравнение двух выборок
Проверяем, принадлежат ли выборки одной генеральной совокупности.
Sм =86,49; Sт = 29,24; ![]() .
.
Уровень значимости уменьшается, значит, выборки принадлежат разным генеральным совокупностям.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.