Механика сплошных сред: Методические указания для выполнения расчетно-графических работ и курсовой работы (Раздел «Напряжения»)

Министерство образования Российской Федерации

Сибирский государственный индустриальный университет

Кафедра технологии и автоматизации

кузнечно-штамповочного производства

МЕХАНИКА СПЛОШНЫХ СРЕД

Методические указания для выполнения

расчетно-графических работ и курсовой работы.

Специальность «Обработка металлов давлением (110600),

Специализация «Кузнечно-штамповочное производство» (110602)

Новокузнецк

2004

УДК 621.73 (07)

Даны методические указания, математические зависимости и примеры выполнения расчетно-графической работы по основному разделу механики сплошных сред: «Напряжения».

Предназначены для студентов специальности «Обработка металлов давлением» (110600), специализация «Кузнечно-штамповочное производство».

Рецензенты – кафедра обработки металлов давлением Сибирского государственного индустриального университета (зав.кафедрой ).

Печатается по решению редакционно-издательского совета университета.

1.  Напряжения

В точке деформированного тела задан тензор напряжений в произвольных осях

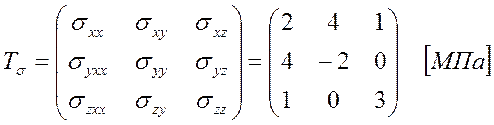
и направляющие косинусы нормали к площадке, наклоненной к координатным плоскостям

;

.

Вычислить:

1.  В произвольных осях координат

1.1.  Третий направляющий косинус.

1.2.  Напряжения на наклонной площадке (полное, нормальное, касательное) и их проекции на оси координат.

1.3.  Инварианты тензора.

1.4.  Шаровой тензор и тензор девиатор напряжений.

1.5.  Инварианты девиатора напряжений.

1.6.  Октаэдрические напряжения.

1.7.  Интенсивность нормальных и касательных напряжений.

2.  В главных осях координат

2.1.  Направляющие косинусы главных осей.

2.2.  Главные нормальные и касательные напряжения.

2.3.  Инварианты тензора.

2.4.  Инварианты девиатора.

2.5.  Интенсивность нормальных и касательных напряжений.

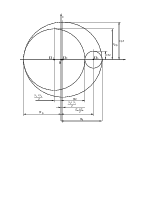
2.6.  Построить диаграмму напряжений Мора.

1. В произвольных осях координат.

1.1.  Третий направляющий косинус

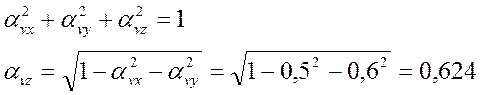
1.2.  Напряжения на наклонной площадке

Проекции на оси координат

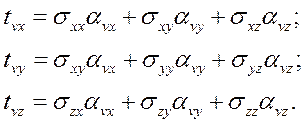
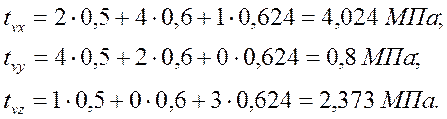
Полное напряжение

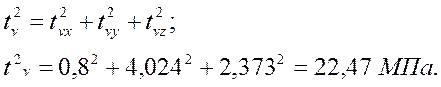
Нормальное напряжение

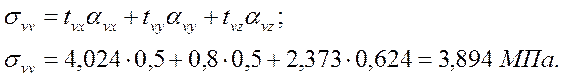
Касательное напряжение

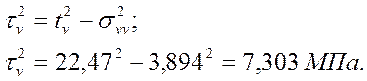
1.3.  Инварианты тензора

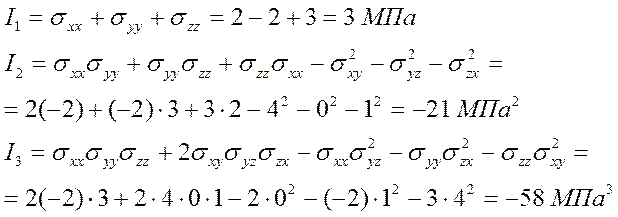
1.4.  Шаровой тензор и тензор девиатор напряжений

Среднее напряжение

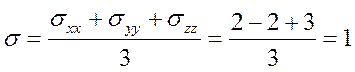
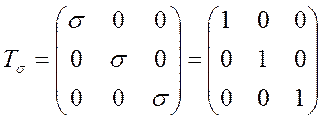
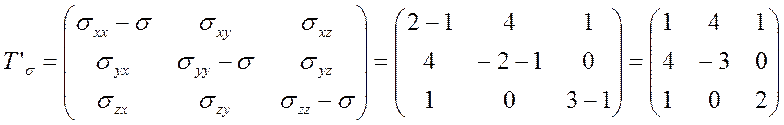
1.5.  Инварианты девиатора напряжений

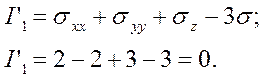
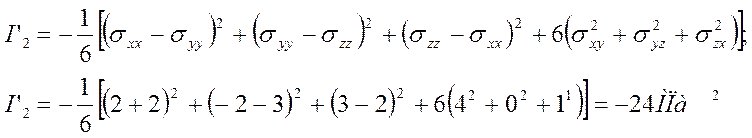
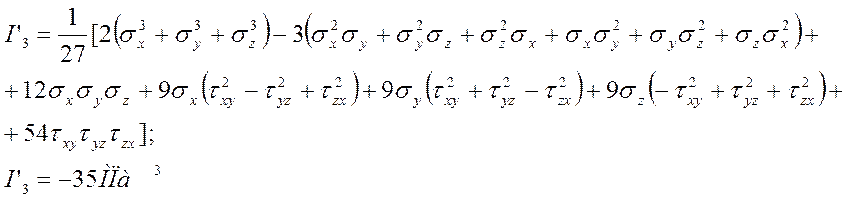Октаэдрические напряжения

Нормальные

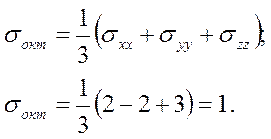
Касательные

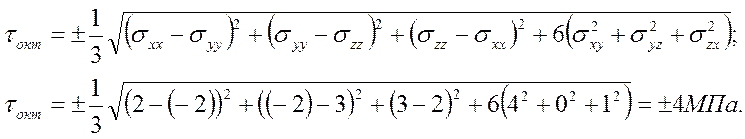
1.6.  Интенсивность нормальных и касательных напряжений

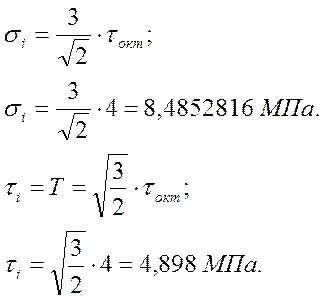
2.  В главных осях координат.

2.1.  Направляющие косинусы главных осей

Составляющие полного касательного напряжения по осям координат

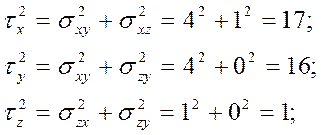
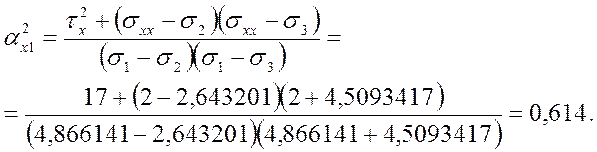
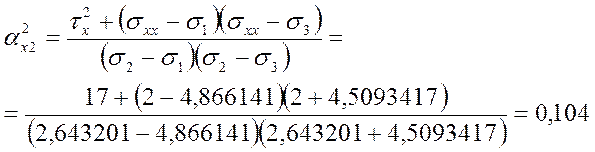
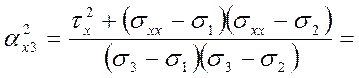
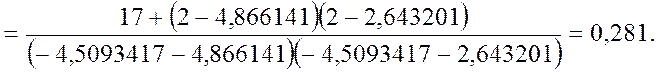
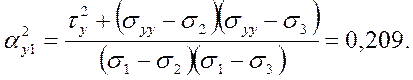
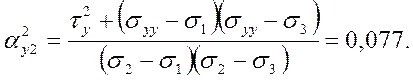
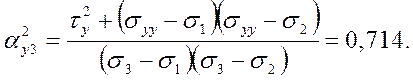
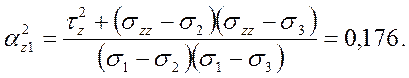
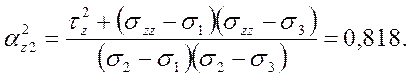
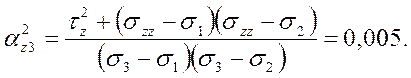
2.2.  Главные нормальные и касательные напряжения

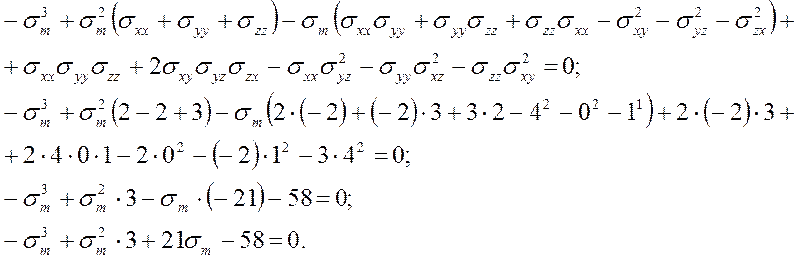Нахождение корней

    .

Главные касательные напряжения

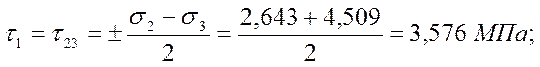
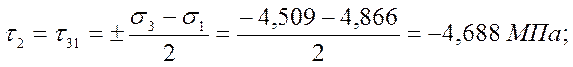
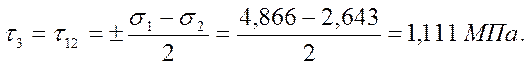
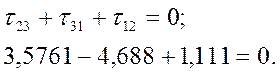
Нормальные напряжения, действующие в площадках главных касательных напряжений

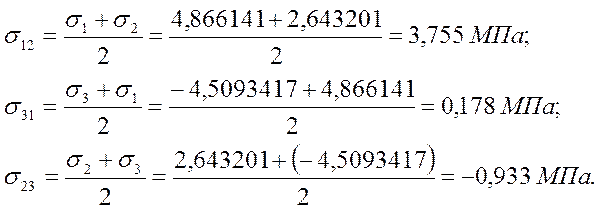
2.3.  Инварианты тензора

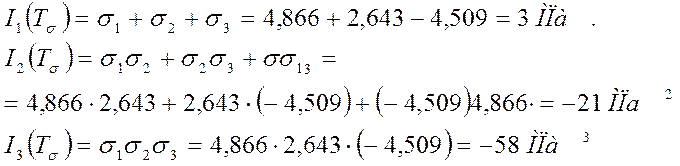
2.4.  Инварианты девиатора

.

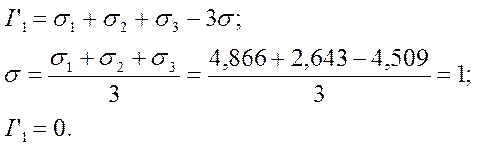
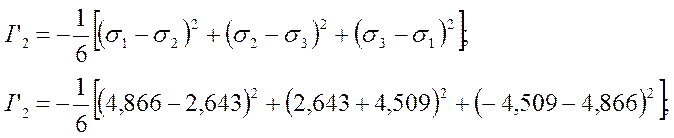
Г₃ =-34,8.

2.5.  Интенсивность нормальных и касательных напряжений

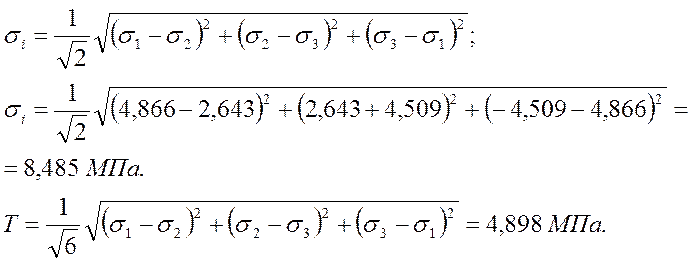
2.6.  Диаграмма напряжений Мора

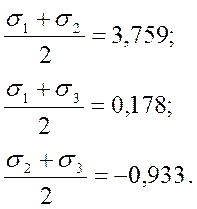
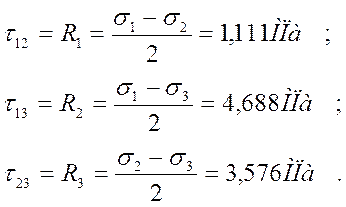
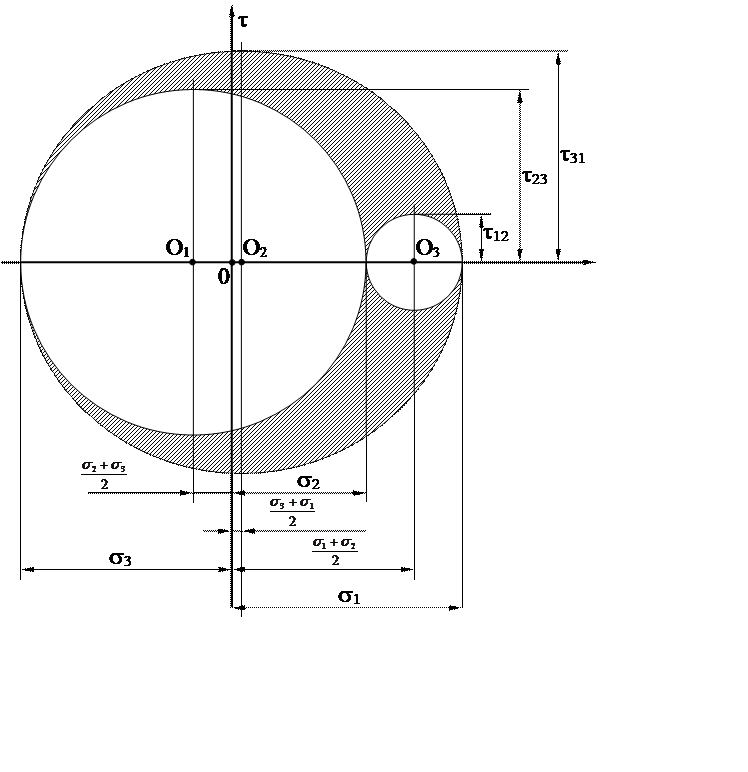
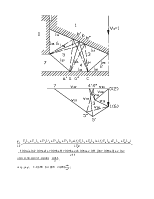
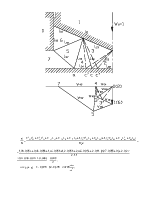
2.  Деформации.

Задан элемент прямоугольной формы с координатами: А(0; 0), В(1; 0), С(0; 1), D(1; 1).

В результате деформации координаты точек стали следующими:

А’(0,1; 0,1), В’(1,05; 0,2), С’(0,11; 1,12), D’(1; 1).

Определить:

1.  Компоненты тензора конечной, малой и истинной деформации. Составить тензоры деформаций.

2.  Для тензора конечной и малой деформаций определить интенсивность растягивающих (сжимающих) деформаций и деформаций сдвига.

3.  Сравнить результаты и сделать выводы о правомерности использования тензора малой деформации.

1.1.  Компоненты тензора конечной деформации

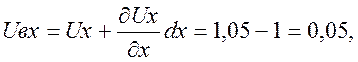
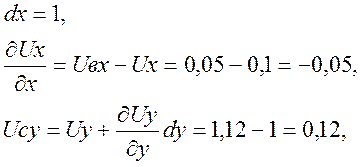
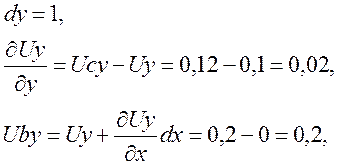
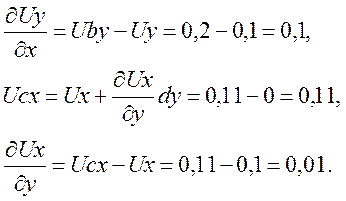
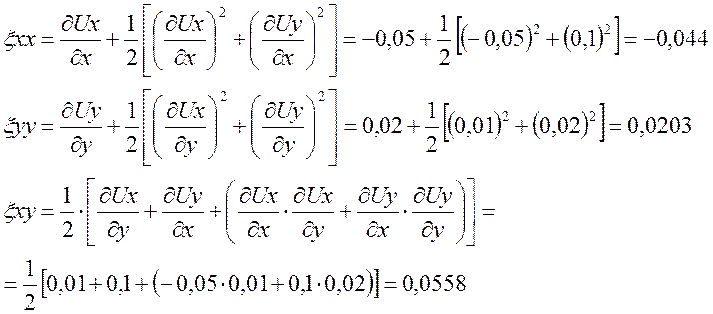
1.2.  Тензор конечной деформации

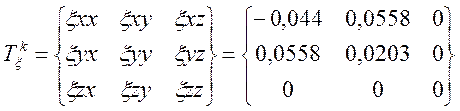
1.3.  Компоненты тензора малой деформации

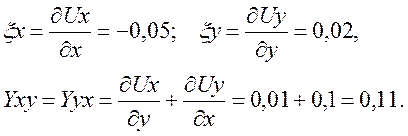
1.4.  Тензор малой деформации.

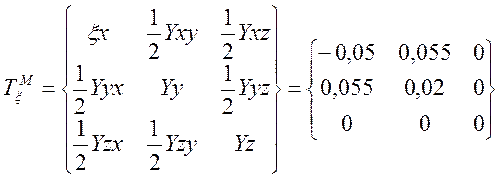
1.5.  Логарифмические деформации

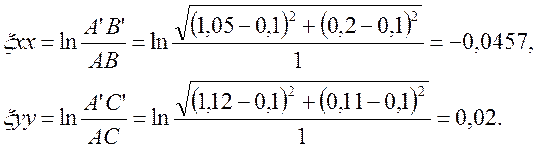
2.1. Интенсивность деформации растяжения (сжатия) для тензора конечной деформации

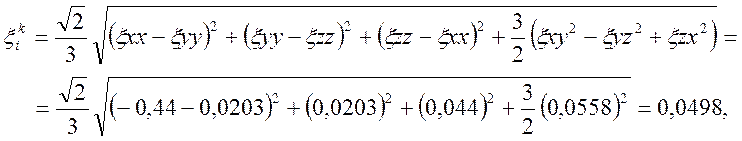
2.2. Интенсивность деформации растяжения (сжатия) для тензора малой деформации

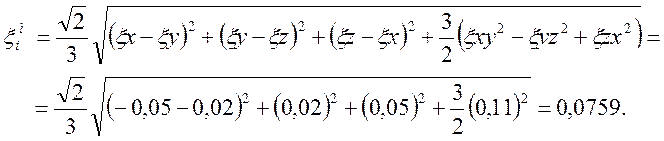
2.3. Интенсивность деформации сдвига конечной деформации

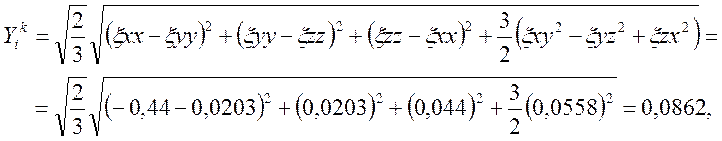
2.2. Интенсивность деформации сдвига малой деформации

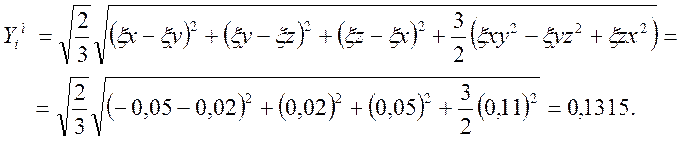
3. Погрешность расчета

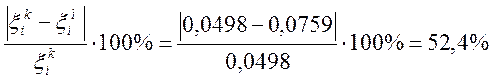
Сравним результаты вычисления интенсивности малой и конечной деформации, видим, что разрыв в их численных значениях превышает 15%.

Из этого следует, что в расчетах для конечной деформации нельзя использовать формулы малой деформации.

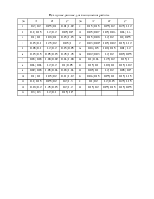
Исходные данные для выполнения работы.