Механика сплошных сред: Методические указания для выполнения расчетно-графических работ и курсовой работы (Раздел «Напряжения»), страница 2

3.  Определение деформирующих усилий методом верхней оценки.

Сущность метода верхней оценки применительно к плоской деформации заключается в том, что объем очага деформации представляется в виде жестких (недеформируемых) треугольных блоков, скользящих один относительно другого и по границам с жесткой зоной. Тем самым действие поле линей скольжения заменяют полем, состоящим из системы прямоугольных отрезков, образующих треугольники. В даль границ блоков  - сторон треугольников – компоненты скоростей перемещений претерпевают разрывы. Внутри каждого блока поле скоростей однородно, т.е. вектор скорости для всех точек данного блока один и тот же. На этом основании строят поле скоростей, при правильном построении всегда является кинематически возможным. Число и размеры треугольных блоков первоначально выбирают произвольно.

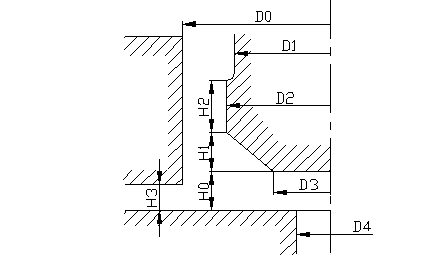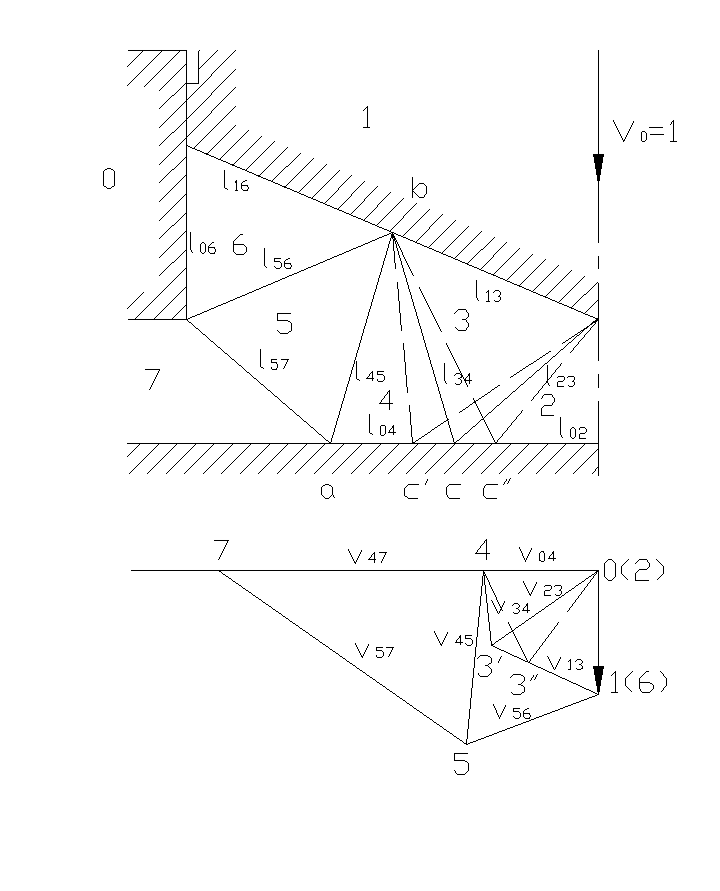
На рисунке 3 представлена общая схема процесса.

	Рисунок 3 – Общая схема процесса

 

Дано: D₀=0,1м ;  D₁=0,08м ;  D₂=0,1м ;  D₃=0 ;  D₄=0 ;  H₀=0,03 м ;  H₁=0,045м;

H₂=0,015м ;  H₃=0,1м ;  H₄=0,032м ;  K=62 мн/м²  ;  f₁=0,11 ; f₂=0,2 .

Определить удельное усилие деформации.

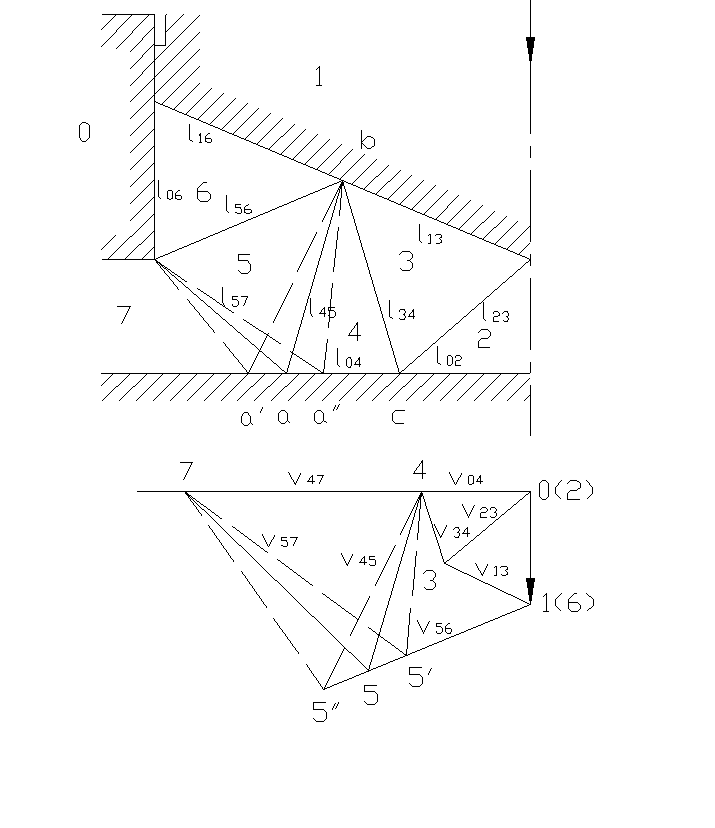
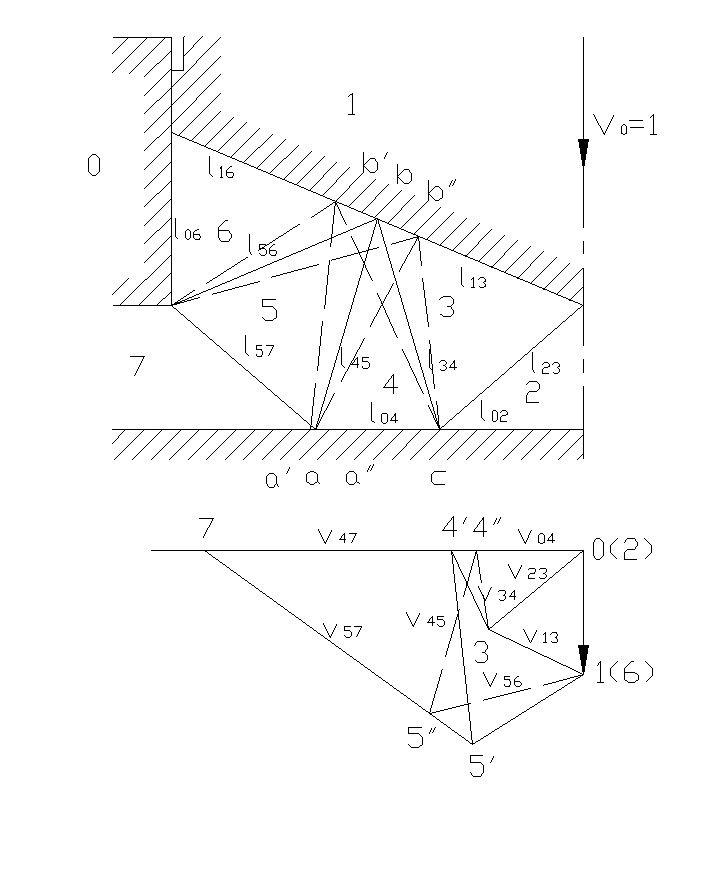
Строим физическую картину процесса в масштабе (рис. 4а). В следствии симметричности поле относительно оси Z на этом рисунке изображена его половина, что достаточно для дальнейших построений и расчетов.

Цифрами обозначаем: О – матрица, 1 – пуансон.

Очаг деформации произвольно делим на треугольные блоки 2,3,4,5,6.

Граница между зонами и блоками определяются двумя цифрами, например 34 – граница между блоками 3 и 4, 13 – контактная поверхность и т.д.

Длину соответствующих границ (линий) обозначаем соответственно L₃₄, L₁₃ и т.п.

Рисунок 4 – Физическая картина процесса и гадограф

а)

б)

Компоненты скоростей блоков, нормальные жесткопластической границе равны нулю. Вдоль границе 23, 34, 45, 56 происходит разрыв скоростей.

Построение годографа.

Годограф представляет собой диаграмму, в которой векторы скоростей перемещения точек деформируемого тела отображаются по величине направлению прямыми отрезками, исходящими из произвольной точки – полюса.

Каждой зоне и каждому блоку на годографе соответствует точка.

Для построения годографа (рис. 4б сплошные линии) от центра О по вертикале отложим вектор О₁ скорости пуансона, длину которого примем за единицу. Далее от конца вектора производим линию, параллельную линии 13 на физической картине процесса, а из точки О линию параллельную линии 23. Пересечение этих линий определяет точку 3, т.е. конец вектора скорости блока 2. Продолжая построение подобным образом далее, получим изображенный на рис. 2б годограф.

Линии годографа обозначают относительные скорости блоков вдоль линий разрыва.

Удельное контактное усилие определяется из выражения:

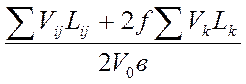=    , где  V_ij – разрывы скоростей течения вдоль границ блоков;

V_k – разрывы скоростей течения вдоль контактов;

L_ij – длина отдельных границ между блоками;

L_k – длина границ между блоками и контактами;

K – пластическая постоянная;

в – ширина проекции контактной поверхность на плоскость перпендикулярную направлению движения инструмента;

V₀ – скорость инструмента.

Принимаем   в=1, V₀=1.

Влияние скорости деформации учтено в пластической постоянной K.

Рассчитываем удельное усилие

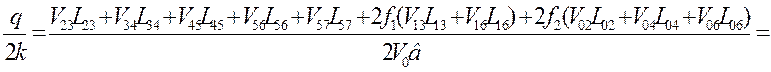
    откуда  .

Так как очаг деформации делим на треугольные блоки произвольно, и метод верхней оценки предполагает нахождение минимальных значений удельных усилий, как наиболее верных, вблизи точка  А  слева и справа обозначим точки А¹ и А¹¹ , построим новую физическую картину процесса и новые годографы (рис. 4 – пунктирные линии) аналогично прежним и подсчитаем удельные усилия q₁ и q₂.

Рисунок 5 – Физическая картина процесса и гадограф

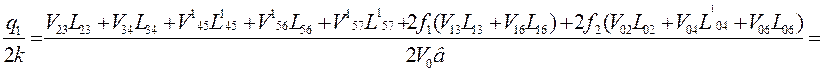
откуда ;

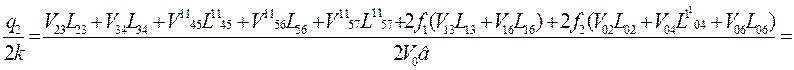
откуда .

Из трех значений q, q₁ и q₂ выбираем минимальное q₁=24,083 и зафиксируем точку а¹.

Далее вблизи точки в слева и справа обозначим точки в¹ и в¹¹ (рис. 5) и, проведя действия аналогичные действиям в точке а, получим удельное усилия q₃ и q₄.

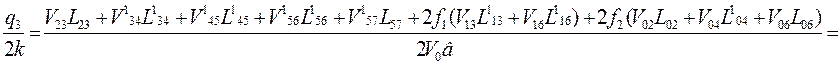
откуда ,

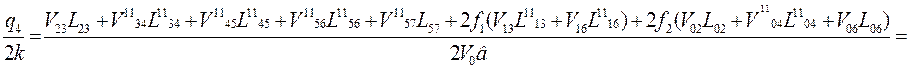
откуда .

Выбираем минимальное значения из величин q₁, q₃ и q₄ – q₁=24,083 и зафиксируем точку в. Аналогичные действия проводим в точке с (рис. 6) и подсчитываем удельные усилия q₅ и q₆.

Рисунок 6 – Физическая картина процесса и гадограф

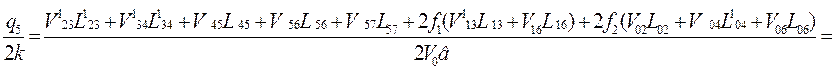
откуда ,

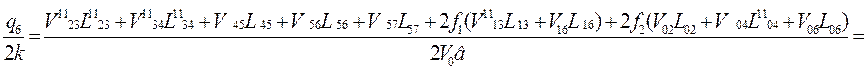
откуда ,

Выбираем минимальное значение удельного усилия из величин q₁, q₅ и q₆: q₁=24,083. Это и будет наиболее вероятное усилие для данного процесса определенное методом верхней отценки.

МЕХАНИКА СПЛОШНЫХ СРЕД