Висячие и вантовые покрытия. Оптимизация висячих и вантовых покрытий, страница 5

Считаем, что уменьшение массы настила или его увеличение компенсируется соответственным увеличением или уменьшением предварительного напряжения и в целом нагрузка на опорные конструкции остается неизменной или не оказывает существенного влияния на массу опорного контура, поддерживающих конструкций, оттяжек. Это предположение позволяет нам ограничиться рассмотрением только вантовой системы и плит покрытия.

Оптимальный шаг вант по опорному контуру определяется по формуле (*). Стоимость материала вант определяется выражением:

Стоимость   плит   покрытия,   приходящихся на один вант, может быть представлена в следующем виде:

Стоимость материала элементов покрытия, участвующих в рассмотрении, определяется из выражения:

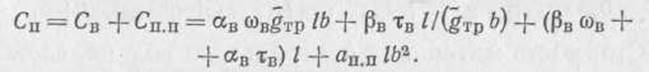
Принимаем обозначения:

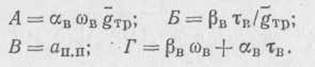
Стоимость элементов покрытия запишется в виде:

   (7)

Продифференцировав уравнение (Х7) и приравняв его нулю, получим выражение для нахождения оптимального шага:

Стоимость материала вант минимальна при шаге:

3.4. Определение оптимального шага двухпоясных Вантовых систем с радиально расположенными вантовыми фермами.

При выводе формулы оптимального шага вант двухпоясных Вантовых систем приняты те же предпосылки и упрощения, что и для однослойных систем с радиальной сеткой вант. Оптимальный шаг вант находим из условия минимума стоимости материала покрытия [формула (*)].

Стоимость всех элементов покрытия, участвующих в рассмотрении, определяется по формуле:

   (8)

Стоимость    материала несущего пояса определяется:

Стоимость материала стабилизирующего пояса определяется:

Стоимость материала центрального кольца, служащего узлом крепления для несущих вант, определяется по формуле:

   (9)

Стоимость кольца, соединяющего    стабилизирующие ванты в центре покрытия, определяется по формуле

   (10)

Диаметр стабилизирующего кольца принят равным диаметру несущего кольца.

Стоимость решетки покрытия определяется по формуле:

Следует отметить, что при подборе сжатой решетки по предельной гибкости стоимость решетки при определении оптимального шага ванта не учитываем. После   подстановки значений в формулу (8) принимаем обозначения:

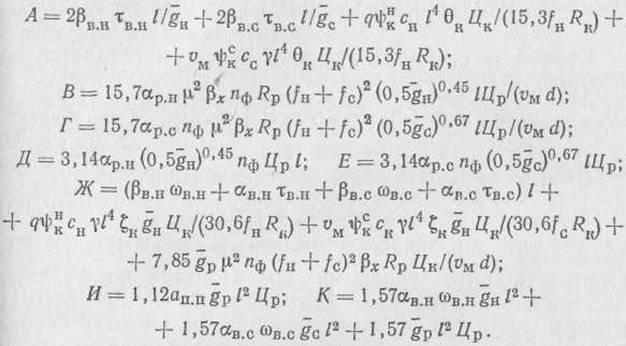
Уравнение  (8)  в новых обозначениях запишется в виде:

   (8’)

Оптимальный шаг двухпоясных систем по стоимости материала получим, продифференцировав выражение (8') и приравняв его нулю:

Решение находится последовательными попытками. При использовании ЭВМ корни уравнения определяются  по стандартной программе.

Оптимальный шаг систем из условия минимума стоимости материала вант может быть определен по формуле:

3.5. Определение оптимального шага параллельно расположенных двухпоясных вантовых систем по стоимости материала.

Оптимальный шаг двухпоясных вантовых системнаходят исходя из тех же предпосылок и упрощений, что и у однопоясных систем. Стоимость элементов покрытия, участвующих в рассмотрении, определяется по формуле:

   (11)

Стоимость несущего пояса определяется по формуле:

   (12)

Стоимость стабилизирующего пояса определяется по формуле

   (13)

Стоимость решетки определяется по формуле

   (14)

Стоимость плит покрытия определяется по формуле С_пп=а_п._п1b². Подставив выражения (12) — (14) в формулу (11), продифференцировав по шагу систем и приравняв нулю, получим выражение для определения оптимального шага вант по стоимости материала покрытия:

   (15)

Выражение (15) преобразуется к кубическому уравнению, решаемому методом попыток:

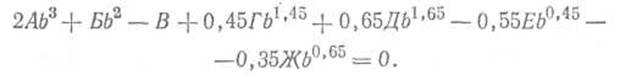   (16)

В выражениях    (Х.102), (Х.103) приняты   обозначения

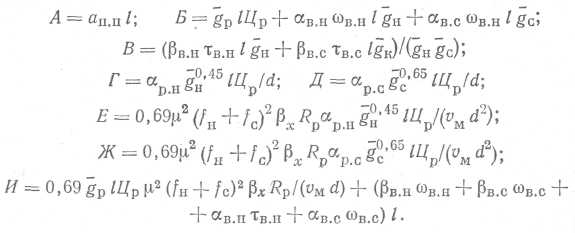
Оптимальный    шаг систем, при котором    стоимость вант минимальна, равен:

Список используемой литературы:

1) Я. М. Лихтарников «Вариантное проектирование и оптимизация стальных конструкций».-М.: Стройиздат, 1979.-319 с., ил.