Висячие и вантовые покрытия. Оптимизация висячих и вантовых покрытий, страница 4

3.2. Определение оптимального шага однослойных висячих покрытий с радиальной сеткой вант.

В данном случае решается задача оптимизации шага вант по опорному контуру из условия минимума стоимости материала покрытия. Это решение не может дать окончательного ответа об оптимальном шаге вант, который получается при минимизации приведенной стоимости покрытия, но может служить первым приближением точного решения.

Изменение шага вант влечет за собой изменение стоимости материала вант, плит покрытия и центрального кольца. Изменение стоимости наружного опорного контура и стоек, поддерживающих покрытие, считаем незначительным и в расчете не рассматриваем. В частности, внешний опорный контур не получит заметного снижения стоимости от уменьшения массы покрытия, так как в этом случае необходимо будет увеличить предварительное напряжение, чтобы обеспечить жесткость покрытия. Данное предположение несправедливо для покрытий, не нуждающихся в создании предварительного напряжения.

Оптимальный   шаг   найдем  из  условия    минимума функции цели — стоимости материала покрытия:

    (*)

где —функция цели — стоимость; С_i — удельная стоимость учитываемых элементов; V_i— объем (масса) учитываемых элементов, являющийся функцией шага вант.

Cтоимость материала вант, а также строительный коэффициент массы и прейскурантную стоимость материала вант можно записать:

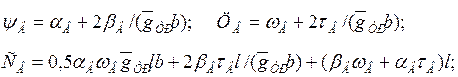 (1)

где  - коэффициенты, получаемые в результате статистической обработки данных по стоимости и строительных коэффициентов массы; g_TР — масса ванта, приходящаяся на 1 м² покрытия при ψ_в=1.

Стоимость центрального кольца определяется:

     (2)

С учетом последней стоимость кольца равняется:

    (3)

где Ц_к — удельная стоимость 1 т материала кольца;  — коэффициенты статистической обработки данных по определению диаметра кольца.

Стоимость плит покрытия принимается из следующих соображений: анализ прейскурантной стоимости показывает, что стоимость 1 м² плит увеличивается с увеличением их длины. Зависимость между стоимостью 1 м² плит и их длиной может быть принята линейной вида С=а_п._пb. Учитывая, что плиты покрытия в радиальном направлении имеют различную длину, а следовательно, и стоимость 1 м² материала, введем предположение, что средняя стоимость материала равна стоимости 1 м² плиты, находящейся в точке, делящей площадь, которая приходится на полупролет ванта, на две равные части. Эта точка расположена на расстоянии х=0,355l от середины ванта. Ширина плиты в этой точке, выраженная через шаг вант по опорному контуру, bi = 0,7lb. Тогда стоимость плит покрытия, приходящаяся на один вант, равна:

   (4)

где а_п._п — коэффициент пропорциональности по стоимости; для плит шириной 1,5 м а_п._п = 0,58, для плит шириной 3 м а_п._п = 0,86.

Суммарная стоимость покрытия и кольца с учетом формул (1), (3), (4) и того, что п_ф=π1/Ь, равна:

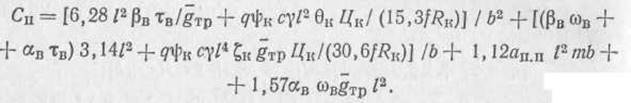    (5)

Примем обозначения:

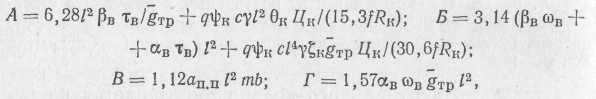
тогда формула (5) примет вид:

Продифференцировав целевую функцию по шагу вант у опорного контура и приравняв производную нулю, получаем выражение для нахождения оптимального шага вант:

   (6)

Преобразовав уравнение (6), приходим к неполному кубическому уравнению, решаемому методом Кар-дано или последовательных попыток:

Из выражения (1) определяем шаг вант, при котором стоимость материала вант минимальна:

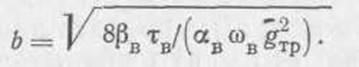
3.3. Определение оптимального шага вант однослойных висячих покрытий из одиночных параллельно расположенных нитей по стоимости материала вант.