Висячие и вантовые покрытия. Оптимизация висячих и вантовых покрытий, страница 3

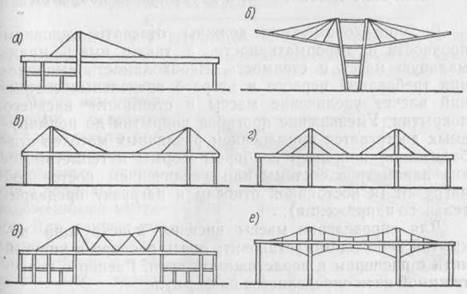
Рис. 4. Комбинированные висячие покрытия

а -  одноконсольные; б — двухконсольные; в, г — вантовая комбинированная система с радиальным и параллельным расположением вант; д — вантовая система с криволинейным верхним поясом и треугольной решеткой; е — висячая система с передачей распора на балку жесткости

5.   Сплошные системы (мембраны). Пролетная конструкция представляет собой тонкий металлический лист, работающий на растяжение и выполняющий роль несущей и ограждающей конструкции (рис. 5).

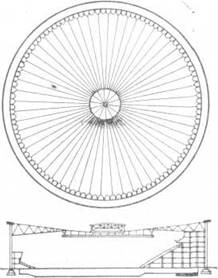
Рис.  5.   Предварительно-напряженное мембранное покрытие           

3. Оптимизация висячих и вантовых покрытий

3.1. Выбор геометрических параметров висячих покрытий, круглых в плане с радиальной сеткой вант

Назначение геометрических параметров покрытия играет важную роль, так как они определяют экономичность здания в целом. В общем случае эта задача решается методами математического программирования. Для частных случаев в виду простоты конструкций висячих покрытий удаётся получить аналитическое решение. Такое решение для однослойных висячих покрытий, круглых в плане с радиальной сеткой вант, получено М.А. Ивановым и

Т.А. Усачевым. Оптимальные по стоимости покрытия получаются при геометрических параметрах, соответствующих минимуму стоимости:

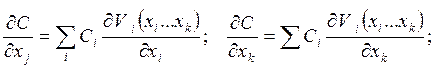
где  - функция цели-стоимости: C_i – удельная стоимость учитываемых элементов; V_i – объем учитываемых элементов, являющихся функцией этих параметров.

Распор, приходящийся на 1м длины опорного контура, расчетные усилия в вантах, сжимающее усилие в контуре и длина вант определялись по следующим формулам:

, где q – расчетная нагрузка; r₀ – радиус покрытия;  остальные обозначения показаны на рис. 6.

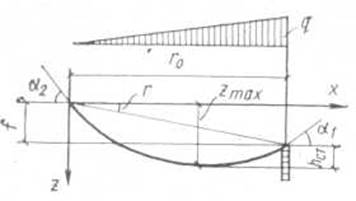
Рис. 6. Расчетная схема покрытия.

Отсюда получены частные случаи: для вогнутой и шатровой систем, системы с равными углами наклона вант на центральном и контурном кольцах.

Покрытия вогнутого типа. Минимальный расход стали   на   ванты покрытия имеет  место  при стрелке провисания . Оптимальное значение стрелки провисания при учете стоимости вант и контурного кольца получается:

где ; С_н.к., , С_в,  - удельная стоимость и расчетное сопротивление на сжатие (растяжение) контурного кольца и вант.

Значительно меньшее значение оптимальной стрелки провисания получается при учете стоимости стен, расположенных выше низшей точки покрытия:

где ; С_с — стоимость 1 м стен.

На выбор оптимальной стрелки провисания покрытия могут существенное влияние оказывать эксплуатационные затраты. Минимум стоимости покрытия с учетом эксплуатационных затрат реализуется при стрелке провисания:

где ; Т, С_в — расчетный срок эксплуатации здания и стоимость эксплуатации 1 м в год.

Покрытия шатрового типа. Оптимальная стрелка провисания с учетом затрат на контурное кольцо и ванты определяется из выражения

с учетом эксплуатационных затрат

где .

Покрытия с равными углами наклона ванта на опорах. Оптимальная стрелка провисания с учетом стоимости вант и опорного контура равна:

то же, с учетом стоимости стен

с учетом эксплуатационных расходов

где

Анализ формул и численных решений позволил М. А. Иванову и Т. А. Усачеву сделать следующие выводы. Учет стоимости эксплуатации в целевой функции значительно снижает стрелку провисания. Так, если стены выполнены из кирпича, она втрое меньше при расчетном сроке эксплуатации 60—90 лет и вдвое при сроке эксплуатации 30 лет; при витраже стрелка почти остается без изменений; без учета эксплуатационных расходов стоимость шатрового покрытия в 5—10 раз меньше вогнутого, с учетом этих расходов только на 5—10% при сроке эксплуатации 30 лет; с учетом эксплуатационных расходов наиболее рациональным оказывается покрытие с равными углами наклона вант; индивидуальное назначение стрелки провисания (подъема) в зависимости от конкретных условий может дать значительный экономический эффект, который особенно проявляется в большепролетных зданиях.