Методы оптимизации в металлургии: Методические указания к выполнению курсовой работы, страница 6

Повторяем проверку выполнение условий (2) и (5) в новой точке. Для проверки условий (5) по свойствам вычисляем значения параметров пластичности и твердости в точке Х_{i, 2}. Условия выполняются, поэтому переходим из точки 2 в следующую точку. Вычисляем координаты точки 3:

Повторяем проверку выполнение условий (2) и (5) в новой точке. Для проверки условий (5) по свойствам вычисляем значения параметров пластичности и твердости в точке Х_{i, 3}. Условия выполняются, поэтому переходим из точки 3 в следующую точку. Вычисляем значения градиента в точке 3:

Вычисляем координаты точки 4:

Повторяем проверку выполнение условий (2) и (5) в новой точке. Для проверки условий (5) по свойствам вычисляем значения параметров пластичности и твердости в точке Х_{i, 4}. Условия выполняются, поэтому переходим из точки 4 в следующую точку. Вычисляем значения градиента в точке 4:

Вычисляем координаты точки 5:

Повторяем проверку выполнение условий (2) и (5) в новой точке. Для проверки условий (5) по свойствам вычисляем значения параметров пластичности и твердости в точке Х_{i, 5}. Условия выполняются, поэтому переходим из точки 4 в следующую точку. Вычисляем значения градиента в точке 5:

Вычисляем координаты точки 6:

Проверка условий по химическому составу (2) показывает, что условие не выполняется, поэтому процесс поиска оптимума дальше не имеет смысла. Формальное решение состоит в том, что координаты точки Х_i, 5 должны быть приняты в качестве оптимального решения. Точка оптимума имеет координаты:

-  кремний  (Si) = 5, 996 масс.% ;

-  медь        (Cu) = 1, 5 масс.% ;

-  магний    (Mg) = 0, 204 масс.% ;

-  марганец (Mn) = 0, 20 масс.% .

При этом получается значения прочности σ_в = 20,05 кгс/см² .

Для сравнения приведем результаты поиска оптимума для данной задачи методом Монте-Карло. Точка оптимума при условиях (2) и (5) имеет следующие координаты:

-  кремний  (Si) = 5, 99 масс.% ;

-  медь        (Cu) = 1, 54 масс.% ;

-  магний    (Mg) = 0, 2 масс.% ;

-  марганец (Mn) = 0, 21 масс.% .

1.4 Метод покоординатного поиска

Метод покоординатного поиска или поочередного изменения координат (именуемый в литературе методом Гаусса-Зейделя), является простейшим методом оптимизации и широко применяется в инженерной практике. При оптимизации этим методом последовательное продвижение осуществляется с помощью поочередного варьирования каждой переменной до достижения частного экстремума параметра оптимизации. Алгоритм поиска следующий:

1.Выбирается исходная точка х₁=(х₁₁, х₂₁, . . ., х_k1) и шаг варьирования  (j = 1, 2, . . .k) по каждой переменной.

2.В первом рабочем цикле поиска оптимума, который осуществляется в направлении координатной оси х1, совершается пробное движение (ставится эксперимент или производятся вычисления) вдоль этой оси в положительном и отрицательном направлении по отношению к направлению оси х1, т.е. определяется величина параметра оптимизации в точках:

(13)

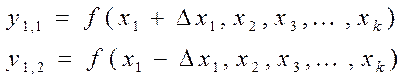
3.Производится сравнение полученных значений параметра у_1,1 и у_1,2   и при поиске максимума выбирается направление возрастание параметра у (при поиске минимума – направление убывания параметра у).

4.Осуществляется 1-й цикл рабочего движения, который состоит в движении вдоль оси x₁ в направлении возрастания (убывания) параметра оптимизации с шагом  и измерением (или вычислением) параметра оптимизации в каждой точке

до тех пор, пока не будет достигнут частный экстремум по этой переменной и пока величина параметра оптимизации не перестанет возрастать. Критерием прекращения i-го рабочего цикла может служит или выполнение неравенства

или выполнение неравенства

где ε – некоторое положительное число, характеризующее точность решения исходной задачи поиска экстремума.