Построение зубчатого зацепления и определение качественных показателей зацепления

3.2 Построение зубчатого зацепления и определение качественных показателей зацепления.

На основании проведенных расчётов строится картина эвольвентного зацепления двух зубчатых колёс, которая отражает способ формирования зубьев при помощи инструментальной рейки.

С учетом масштаба (2:1) построения на чертеже отмечаем положения осей вращения колёс О₁ и О₂, и проводим межосевую линию 0₁0₂. Из центров вращения проводим окружности впадин и вершин зубьев, делительные и основные окружности. Начальные окружности   должны касаться друг друга в точке пересечения с межосевой линией, то есть в полюсе зацепления. Через полюс зацепления (точка Р) проводим общую касательную t-t к начальным окружностям, которая должна быть перпендикулярна к межосевой линии. К основным окружностям проводим общую касательную n-n, являющаяся производящей прямой профилей зубьев и являющаяся линией зацепления. Участок линии зацепления n-n между точками её касания N₁ и N₂ с основными окружностями получил название теоретической линии зацепления. Участок линии зацепления, заключённый между точками а и b ее пересечения с окружностями вершин зубьев, представляет собой рабочую линию зацепления.

Порядок построения профилей зубьев зубчатых колёс, которые касаются друг друга в полюсе зацепленияР:

Эвольвентный профиль зуба образуется как траектория точки, принадлежащей линии зацепления n-n и совпадающей в данный момент с точкой Р при качении без скольжения линии зацепления по основной окружности. Начальная точка эвольвентной части профиля зуба лежит на основной окружности, а конечная точка - на окружности вершин зубьев.

В первую очередь определяем положение начальной точки эвольвенты на основной окружности 1^╹. Для этого можно использовать приближённый графический метод, дающий достаточную точность. Дугой радиуса 3/4 PN из центра, расположенного на отрезке PN и удаленного на 1/4 PN от точки N проводим засечку на основной окружности. Это и есть начальная точка 1^╹ эвольвентного профиля зуба.

Далее отрезок PN разбиваем на несколько равных отрезков, a дугу l'N на столько же равных между собой частей. Точки, полученные при делении отрезков, обозначают по порядку, начиная от Р и 1^╹ цифрами 2, 3, ... и 2', 3', ... соответственно. Далее проводим касательную к основной окружности в точке 2' и, используя свойства эвольвенты, откладывают на ней от точки 2' отрезок, равный 2Р, затем проводят касательную к основной окружности в точке 3' и откладывают на ней от точки 3' отрезок, равный ЗР и т.д. Соединив полученные точки на касательных, получают эвольвентный профиль зуба от точки 1' на основной окружности до полюса Р. Покатив прямую NN далее за точкой N и выполнив аналогичные построения, получим отрезок профиля от полюса Р до окружности вершин зубьев. Для получения нерабочей части профиля ножки зуба от основной окружности до окружности впадин зубчатого колеса формируем галтель зуба, для чего сопрягаем эвольвенту с окружностью впадин дугой окружности с радиусом  Противоположный профиль зуба строится симметрично относительно оси зуба. Для построения остальных зубьев определяем угловой шаг

    ;;

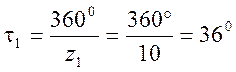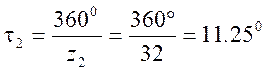откладываемих по разные стороны построенного профиля зуба и, используя вырезанные по полученному профилю зуба шаблоны, строим остальные зубья, обычно по три зуба каждого колеса. Описанные построения проводим как для первого, так и  для второго колеса.

На построенных зубьях отмечаем участки профилей, контактирующие в процессе работы зубчатого зацепления (активные профили), для чего радиусом    О₁а и O₂b проводим дугу до пересечения с профилем сопряжённого колеса. Активный профиль (от полученной точки до окружности вершин) отмечаем штриховкой.

Для построения дуг зацепления, необходимо через крайние точки А₁ и С₁ рабочего участка профиля первого колеса провести в направлении вогнутости нормали к этому профилю (они являются касательными к основной окружности первого колеса). Находим точки а₁ и с₁ пересечения этих нормалей с начальной окружностью первого колеса. Дуга а₁с₁ является дугой зацепления на начальной окружности первого колеса. Аналогично находим дугу зацепления а₂с₂ на начальной окружности второго колеса.

Длина k дуги зацепления определяется по формуле

,

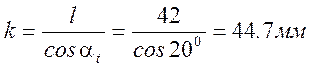где l – длина активной линии зацепления, мм.

Определяем коэффициент торцового перекрытия  из графического построения зацепления колёс:

,

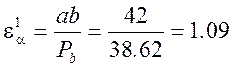где ab – длина активной линии зацепления, мм;

P_b – основной шаг, мм.

Определение коэффициентов относительного скольжения.

Коэффициенты  и  относительного скольжения определяются по формулам:

;  ;

    ;   ;

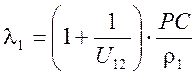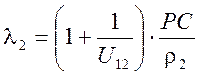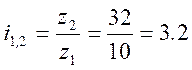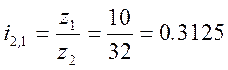x – расстояние от точки N₂ касания теоретической линии зацепления с основной окружностью первого колеса, отсчитываемое в направлении к точке N₁.

Пользуясь данными формулами составим таблицу 1 значений  и .

	Таблица 1. Значения коэффициентов  и .

 

X	0	7	14	21	P	28	35	42
l1	0.6	0.5	0.35	0.14	0	-0.1	-0.8	-2.2
l2	-0.48	-0.3	-0.17	-0.05	0	0.05	0.14	0.2

Пользуясь данными, приведенными в таб. 1, строим диаграммы для значений коэффициентов  и в прямоугольной системе координат.

Для того, чтобы выделить те части диаграмм, которые дают значения  и  для фактически имеющихся на зубьях рабочих участков профилей, нужно через точки а и b провести перпендикуляры к линии зацепления, которые отсекут на диаграммах интересующие нас участки.

Далее строим круговые диаграммы, откладывая от соответствующих точек рабочих участков профилей зубьев на концентрических окружностях дуги, равные (или пропорциональные) ординатам прямоугольных диаграмм.