Определение длины световой волны квантового генератора с помощью эталона Фабри-Перо (Лабораторная работа № 12), страница 2

                                             .                                      (4)                                               

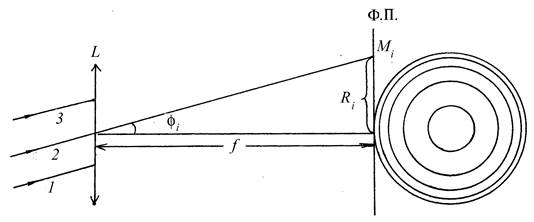
Лучи 1, 2, 3, …, соответствующие углу падения  j_i  и расположенные в плоскостях, параллельных в плоскости чертежа, соберутся в фокальной плоскости объектива в точке М_i, расположенной на угловом расстоянии j_i от осевой линии (рис.2 и рис.3). Аналогичная картина будет наблюдаться для лучей с таким же углом падения j_i, по параллельным плоскостям, проходящим через осевую линию не параллельно плоскости чертежа (по другому азимуту). Это приводит к тому, что множество светлых точек М_i образуют в фокальной плоскости объектива светлое кольцо радиуса R_i.

Из соотношения (4) следует, что разным значениям порядка интерференции m_i, будут  соответствовать разные значения j_i, а следовательно, и разные радиусы

Рис. 3 .

В целом интерференционная картина представляет собой систему концентрических колец, которые получили название полос равного наклона. Соотношение (4) показывает, что максимальное целочисленное значение порядка интерференции mпринадлежит внутреннему кольцу и уменьшается к периферии интерференционной картины. При обработке интерферограммы не имеется возможности непосредственным отсчетом определить m_i для того или иного кольца. В этом случае счет кольцам удобнее вести от центра к периферии интерференционной картины. Найдем связь между порядком интерференции m_i и значением  i, приписывая самому внутреннему кольцу i = 0, а m = m₀ .

Рис. 4 .

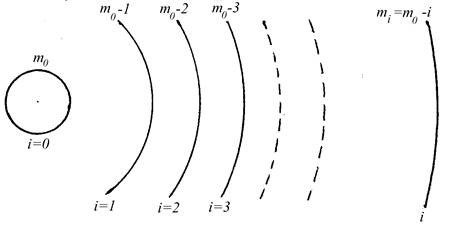
Из рис.4 следует, что m_i = m₀ - i . В этом случае соотношение (4) для произвольного кольца запишется

2tn×cosj_i =(m₀ - i)l  .                                         (5)                                                    

В то же время для центра картины (j = 0) m  не обязательно равно целому числу и в общем случае оно равно (m₀ + e), где  е – дробная часть  0 £ е £ 1, так что для центра

2tn = (m₀ + e)l  .                                              (6)                                                           

Сравнивая соотношения (4) и (6) легко заметить, что если в соотношении (4) m и l - независимые друг от друга переменные, то в соотношении (6) m₀ и l взаимозависимы так, что определенному m₀ соответствует вполне определенная l₀ и  е = е₀ . В этом случае любую меняющуюся l надо рассматривать как величину, отличающуюся от l₀, то есть l = l₀±Dl.

С учетом сказанного соотношения (6) можно записать

        2tn = (m₀ + e₀)l₀  .                                           (6а)                                                      

Используя соотношения (5) и (6а), получим

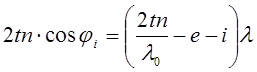                                    .                                  (7)                                              

Если  излучение является монохроматическим, то l = l₀ и соотношение (7) запишется

 ,       или     2tn(1 - cosj _i)=(i + e₀)l₀  .

Для малых углов j 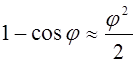   ; с другой стороны из рис.3 следует, что для  i-го кольца  . В этом случае соотношение (7) принимает вид

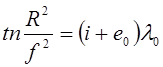                                             ,                                               (8)

или

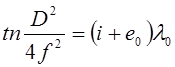                                           ,                                        (8а)

где D – диаметр кольца. Продифференцировав соотношение (8), получим

 .                                         

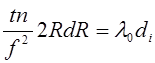Так как при переходе от одного кольца к другому iменяется на 1, то

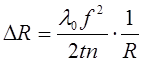                                                 ,                                               (9)

отсюда следует, что по мере увеличения радиуса кольца располагаются все теснее друг к другу.

Распределение интенсивности в полосах интерферометра Фабри-Перо