условию задачи нас интересуют интервалы со знаком минус: 
.
Ответ: .
2) Решить неравенство: 
.
Решение:
1. Найти нули числителя и знаменателя, для этого нужно числитель и знаменатель приравнять к нулю:
; х
+ 8 = 0;
,х = – 8;
так как нет действительных корней, значит нет точек пересечения параболы с осью Ох. Ветви параболы направлены вверх, значит, функция будет принимать положительные значения при любом действительном значении х.
2. Знак неравенства в интервалах будет зависеть от
знака, который будет принимать знаменатель дроби. На координатной прямой отметить
точку х = – 8, учитывая, что знаменатель не равен нулю. Найдем знаки в
интервалах:
+ х
– – 8
3. По условию задачи нас
интересуют интервалы со знаком плюс: 
.
Ответ: .
3) Решить неравенство: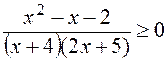 
.
Решение:
1. Найти нули числителя и знаменателя, для этого нужно числитель и знаменатель приравнять к нулю:
; х
+ 4 = 0 или 2х + 5 = 0;
По теореме Виета: х = – 4 х = - 2,5.
, отсюда
и 
.
2.
Разложить числитель и знаменатель дроби на множители (
, где 
и
корни квадратного уравнения):
3. На координатной прямой отметить нули числителя и знаменателя, учитывая, что знаменатель не равен нулю. Найдем знаки в интервалах:
 |
+ + +
- 4 - - 2,5 - 1 - 2 х
По условию задачи нас
интересуют интервалы со знаком плюс: 
.
Ответ: .
4) Решить неравенство: 
.
Решение:
1. Найти нули числителя и знаменателя, для этого нужно числитель и знаменатель приравнять к нулю:
х = 2 или х = - 3 х = - 2 или х = 5;
2. На координатной прямой отметить нули числителя и знаменателя, учитывая, что знаменатель не равен нулю. Найдем знаки в интервалах:
|
+ + +
-
3 - - 2 2 - 5 х
По условию задачи нас
интересуют интервалы со знаком минус: 
.
Ответ: .
5) Решить неравенство: 
.
Решение:
1. Найти нули числителя и знаменателя, для этого нужно числитель и знаменатель приравнять к нулю:
х = - 2 или х = 4 х = 6;
2. На координатной прямой отметить нули числителя и знаменателя, учитывая, что знаменатель не равен нулю. Найдем знаки в интервалах:
 |
+ +
- - 2 4 - 6 х
По условию задачи нас
интересуют интервалы со знаком плюс: 
.
Ответ: .
Решить неравенство:
1)
.
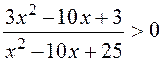Ответ: 
.
2)
.
Ответ: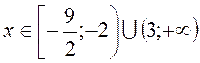 
.
3)
.
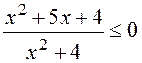Ответ: 
.
4)
.
Ответ: 
.
5)
Ответ: 
.
Задача
1: В прямоугольном треугольнике АВС высота, проведенная к гипотенузе
делит ее на два отрезка AH = 2 и BH = 3, угол В равен 300.
Найти S треугольника. В
Решение:
Н
АВ = 2 + 3 = 5; С А
АС = 
АВ, так как лежит против
угла в 300.
По теореме Пифагора ВС
= 
.
S =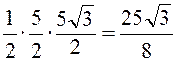 
(ед2).
Ответ: S = 
(ед2).
Задача 2: В прямоугольной трапеции боковая сторона равна большему основанию и составляет с ним угол 600. Найти площадь трапеции, если ее большее основание равно 4 см.
Решение:
Рассмотрим треугольник ВНС.
Угол
ВСН по условию равен 600, значит А В
угол НВС равен 300.
Д С
Н
НС = 
ВС = 2, так как лежит против
угла в 300.
АВ = ДН = ДС – НС = 4 – 2 = 2.
По теореме Пифагора найдем высоту трапеции
ВН = 
= 
= 
.
S
= 
(ДС + АВ)
=
(см2).
Ответ: S = (см2).
Задача 3: Угол между диагоналями прямоугольника равен 1200. Длина диагонали равна 6 см. Найти площадь прямоугольника.
Решение:
Рассмотрим
треугольник АОВ.
В С
ВО = АО = 3 см, т.к. диагонали О
прямоугольника пересекаются и точкой пересечения делятся пополам. А Д
АОВ = 1800 – 1200 = 600.
Треугольник АОВ равносторонний, т.к. у него все углы равны по 600
(ОАВ = АВО
= 
), значит
АВ = 3см.
Рассмотрим прямоугольный треугольник АВД. По теореме Пифагора найдем сторону АД:
АД = 
= 
= 
.
S
= АВ 
= 
(см2).
Ответ: S = (см2).
Задача
4: В прямоугольном треугольнике АВС гипотенуза равна 6
см, а один из углов равен 300. Найти биссектрису прямого
угла треугольника.
Решение: В
АВ = 6
см, 
, значит sin
= 
.
Выразим АС = АВ×sin = 
= 3
см. Д
С А
В треугольнике АДС угол СДА равен 1800 - 450
- 600 = 750. По теореме синусов получаем: 
= 
,
СД = 
= 
.
Ответ: СД = (см).
Задача
5: Острый угол ромба относится к величине тупого угла как 1:2. Высота ромба
равна 
. Найти периметр ромба.
D C
Решение:
Пусть DE = -
высота ромба АВСD.
Пусть 
.
AEB
Если 
,
то 
и так как эти углы внутренние
односторонние, то их сумма равна 1800, т.е. имеем уравнение х
+ 2х = 180, 3х = 180, х = 60.
Значит, 
.
Из треугольника АЕD:
sin 
= 
, откуда находим АD = 
= 
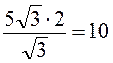, тогда РАВСD = 4×АD = 40.
Ответ: РАВСD = 40.
Решить задачи:
1) Диагональ прямоугольника равна 5 см, а периметр 14 см. Найти стороны прямоугольника.
Ответ: 4 и 3 см, или 3 и 4 см.
2) В равнобедренном треугольнике высота, опущенная на основание равна 6 см., которое равно 6 см. Найти высоту треугольника, опущенную на боковую сторону.
Ответ: 
см.
3) В ромбе АВСД угол АВС равен 600, диагональ АС равна 4 см. Найти периметр и площадь ромба АВСД.
Ответ: Р = 16
см, S = 
см2.
4) В равностороннем треугольнике высота равна 2 см. Найти площадь треугольника.
Ответ: S = 
см2.
5) В параллелограмме АВСД диагональ АС равна 10, диагональ ВД равна 6, сторона АВ равна 5. Найти сторону ВС.
Ответ: 
см.
Определение. Модуль
функции f(x) равен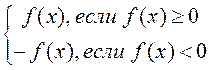 
и в соответствии
с этим разбит случаи, когда |f(x)| = f(x) когда |f(x)|
= – f(x).
Решить уравнение:
1) |1,5x – 2,5| + 2x + 3 = 0; |*2;
|3x – 5| + 4x + 6 = 0; |*2;
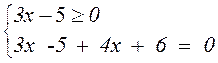
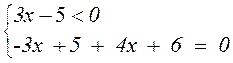
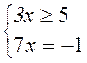
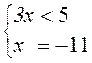
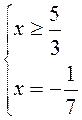
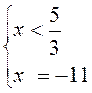
условие не выполнимо, условие выполнимо, подходит не подходит
Ответ: х = – 11.
2) |– 5x + 2| – 3x = 16;
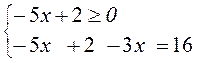
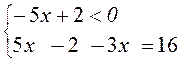
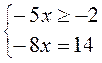
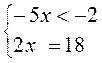
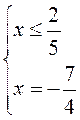
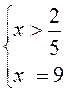
условие выполнимо, подходит условие выполнимо, подходит
Ответ: х1 =
9, и 
.
3) |3x - 2| + 5x + 4 = 0;
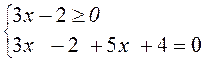
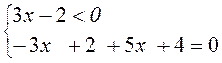
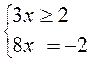
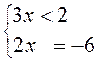
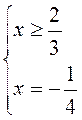
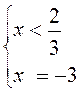
условие не выполнимо, условие выполнимо, подходит не подходит
Ответ: х1 = - 3.
4) |1 – 2x| + 4x = 7;
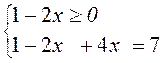
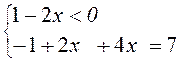
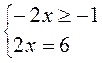
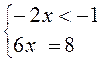
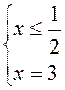
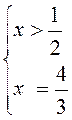
условие не выполнимо, условие выполнимо, подходит не подходит
Ответ: 
.
5) |3 – 2x| + 6x = 7;
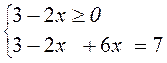
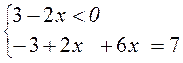
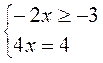
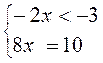
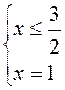
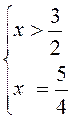
условие выполнимо, подходит условие не выполнимо, не подходит
Ответ: х = 1.
Решить уравнения:
1) 2|1,5x – 1| +5x +4 = 0.
Ответ: х = – 3.
2) |x – 3| = – 7x –4.
Ответ: х = – 
.
3) |3 – x| = 3x + 3.
Ответ: х = 0.
4) |2x – 3| + 5x = 4.
Ответ: х = 
.
5) |0,1x – 0,2| + 1 = x.
Ответ: х = 
.
Решение примерного экзаменационного билета
1.
Вычислить: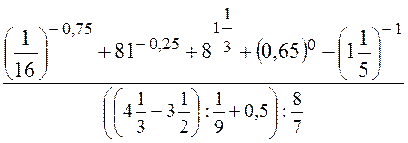 
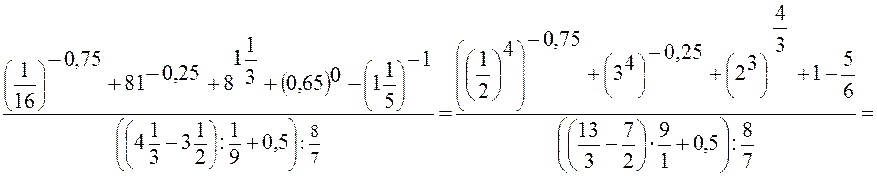
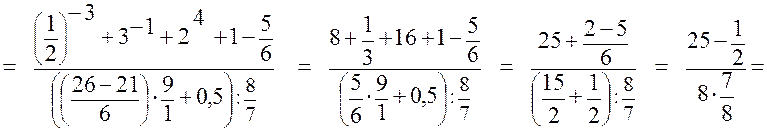
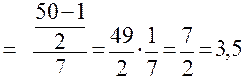
2.
Доказать тождество: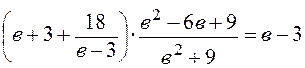 
;
;
;
;
.
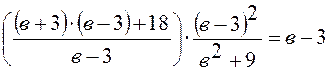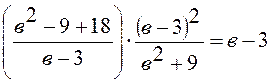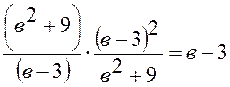3.
Решить систему уравнений: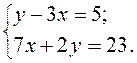 
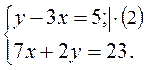
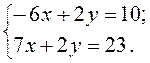
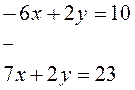
- 13 х = -13
х = 1
;
;
.
Ответ: х = 1, .
4.
Решить неравенство: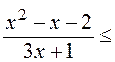 
0
Решение:
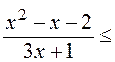0;
3х
+ 1 = 0
х1 = 2; х2 = -1 х3
= 
- + - +
- 1 2
х
Ответ:.
5. Решить задачу: Площадь равнобедренного треугольника равна 39 см2. Противолежащий основанию угол между медианами, проведенными к боковым сторонам равен 900. Найти основание треугольника.
В
Дано
DАВС – равнобедренный
АС – основание
АМ, СД – медианы Д О М
О – точка пересечения медиан АМ и СД
ÐАОВ = 900
S = 39 см2 А С
Найти основание АС. Н
Решение:
Пусть АС = х, тогда 39 = 
. Медианы
треугольника пересекаются и точкой пересечения делятся в отношении 2 : 1 от
вершин.
DАНО – прямоугольный и равнобедренный, следовательно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
