Теорема Пифагора. Расчет косинуса острого угла прямоугольного треугольника: Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

–Г. Отрезок ВD  — проекция наклонной AC. 

4. Дан прямоугольный треугольник ABC, у которого AC = 8 м, ВС = 15 м, АВ = 17 м. Стороны AC, СВ и АВ уменьшили одновременно втрое и получили новый треугольник А₁В₁С₁. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Косинус угла В₁ равен .

–Б. cos  Ð В₁ = cos Ð В.

–В. cos Ð В₁ = .

+Г. cos Ð В₁ = cos Ð В.

5. В прямоугольном треугольнике АВС гипотенуза АВ = 20 мм, катет ВС = 12 мм. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. (ВС + AC)² = АВ².

–Б. BC² + AB² = AC². 

+В. AC = 16 мм.

–Г. Периметр треугольника меньше 45 мм.

6. В параллелограмме ABCD из вершины угла C опущен перпендикуляр CK на диагональ BD, AB = 3 дм, AD = 5 дм. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

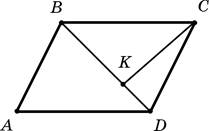
+А. АD² = BK² + CK².

+Б. СK меньше 3 дм.

–В. DK может быть больше 3 дм.

–Г. ВK может равняться KD.

7. В прямоугольном треугольнике АВС катеты AC = b, ВС = а, гипотенуза АВ = с, CD  — высота АD = с₁, DB = с₂, CD = h, a < b. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. cos ACD = .

+Б. .

+В. Ð CAB =  DCB. 

+Г. cos Ð CAB = .

8. Диагонали ромба ABCD равняются: AC = 8 м, BD = 6 м. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. АB = 10 м.

–Б. AC² + BD² = 2AB².

–В. BD = 14 м.

–Г. cos Ð BAC = .

9. Даны две окружности с радиусами R и r, которые касаются извне, d — расстояние между центрами окружностей, l — длина общей касательной, которая не проходит через точку касания окружностей. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Если R ¹ r, то d ¹ l.

–Б. Если R ¹ r, то R + r = l.

+В. .

+Г. .

10. В прямоугольном треугольнике АВС угол С — прямой, CD — высота, cos BCD = . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. .

+Б. cos²  ABC + cos²  BCD = 1.

+В. cos  ABC = .

–Г. . 

11. Сторона равностороннего треугольника АВС равна a. Высоту треугольника обозначили h, радиус вписанной окружности — r, радиус описанной окружности — R. Отметьте, какие из следующих четырех утверждений правильные, а какие  — неправильные.

–А. .

+Б. .

+В. R = 2r.

+Г. .

12. Даны точки A, B, C, и D. Точки A, B  и C лежат на одной прямой, точка D — вне этой прямой. Отрезок CD перпендикулярен АВ, DА : DВ = 5 : 7, CA = 4 дм, CB = 6 дм. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. DA² – AC² > DB² – CB².

+Б. DВ – DА < 2 дм.

–В. AD > 5 дм. 

+Г. дм.

Вариант 2

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.

1. Дан прямоугольный треугольник с гипотенузой АВ = 10 см и катетами AC = 8 см, СВ = 6 см. Учитывая, что косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе, выберите правильное утверждение.

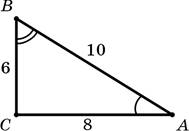
+А. Косинус угла А треугольника равен .

–Б. Косинус угла А треугольника равен .

–В. Косинус угла А треугольника равен .

–Г. Косинус угла А треугольника равен .

2. В прямоугольном треугольнике ABC катет AC = 15 см, гипотенуза AB = 17 см. Выберите правильное утверждение.

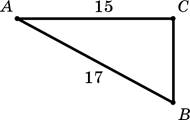
–А. ВС² = AC² – АВ².

+Б. ВС² + AC² = АВ².

–В. ВС > AВ.

–Г. Катет ВС < 8 см.

3. В треугольнике АВС сторона AC = 8 м, сторона ВС = 3 м. Выберите правильное утверждение.

–А. Сторона АВ может быть равной 15 м.

+Б. Сторона AB треугольника АВС может быть равной 7 м.

–В. Сторона АВ может быть меньше 4 м.

–Г. Сторона АВ может быть больше 11 м.

4. Дан прямоугольный треугольник ABC, у которого AC = 8 м, ВС = 15 м, АВ = 17 м. Стороны AC, СВ и АВ увеличили одновременно втрое и получили новый треугольник А₁В₁С₁. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. .

+Б. cos ÐА₁ =  cos Ð A.

+В. Косинус угла А₁ равен .

–Г. cos ÐА₁ = 3 cos Ð A.

5. В прямоугольном треугольнике ABC катет BC = 10 см, гипотенуза