строить и узнавать графики простейших тригонометрических функций и характеризовать их свойства.
Вариант 1
Записывая ответы на задания теста, обведите буквы, отвечающие
утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие
утверждениям, которые вы считаете неправильными. Например, если вы считаете
правильными утверждения А и В, а неправильными — утверждения Б и Г,
запишите 
. Если хотя бы одна буква из
4-х будет не отмечена, задание считается невыполненным.
1. Задана функция y = 
. Выберите правильное утверждение.
–А. Область определения этой функции — все действительные числа.
–Б. Область определения этой функции: х = 1.
–В. Область определения этой функции задается условием: х ¹ 0.
+Г. Область определения этой функции задается условием: х ¹ 1.
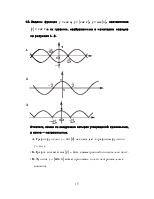
2. На рисунке изображен график функции y = sin x. Выберите правильное утверждение.
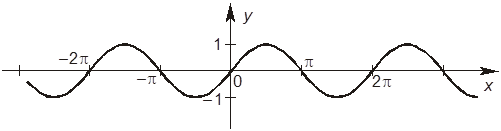
–А. Областью определения функции y = sinx является промежуток [–1; 1].
+Б. Множеством значений функции y = sinx является промежуток [–1; 1].
–В. Наибольшее значение функции y = sin x равно 2.
–Г. Наименьшее значение функции y = sin x равно 0.
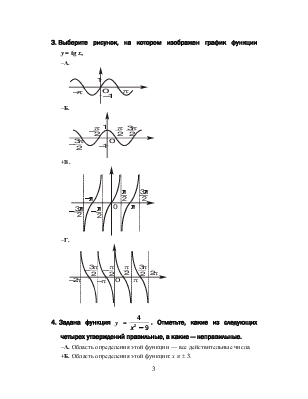
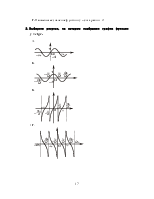
3. Выберите рисунок, на котором изображен график функции y = tg x.
–А.
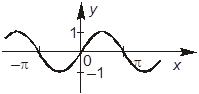
–Б.
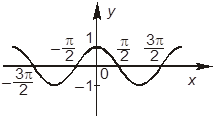
+В.
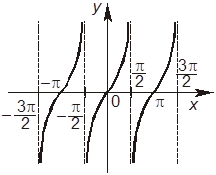
–Г.
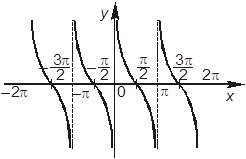
4. Задана функция y = 
. Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
–А. Область определения этой функции — все действительные числа.
+Б. Область определения этой функции: х ¹ ± 3.
–В. Заданная функция нечетная.
+Г. Заданная функция четная.
5. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. 30° = 
.
+Б. Если ÐАОС = 30°, то синус 30° — это ордината точки А единичной окружности (точка С лежит на положительной полуоси x, точка O — начало координат).
–В. sin = –
.
+Г. sin 
= –1.
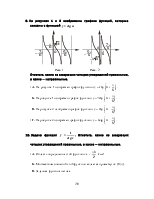
6. На рисунках 1 и 2 изображены графики функций, которые связаны с функцией y = cos x.
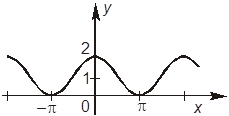
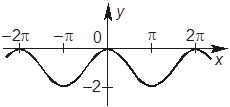
Рис. 1 Рис. 2
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. График функции y = cos x + 1 можно получить из графика функции y = cos x параллельным переносом вдоль оси х на +1 (то есть вправо).
+Б. График функции y = cos x – 1 можно получить из графика функции y = cos x параллельным переносом вдоль оси y на –1 (то есть вниз).
+В. На рисунке 1 изображен график функции y = cos x + 1.
+Г. На рисунке 2 изображен график функции y = cos x – 1.
7. Задана функция y = tg 2x. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Область определения этой функции: х ¹ 
, где kÎZ.
–Б. График этой функции можно получить из графика функции y = tg x, растянув его в два раза вдоль оси y.
+В. График этой функции можно получить из графика функции y = tg x, сжав его в два раза вдоль оси х.
–Г. График
заданной функции пересекает ось х в точках,
для которых х = 
,где kÎZ.
8. Отметьте, какие из следующих четырех утверждений относительно свойств тригонометрических функций, связанных с функцией y = cos x, правильные, а какие — неправильные.
+А. Существует
бесконечное множество значений переменной х,
для которых cos х = 
.
+Б. На промежутке (0; p) функция y = cos х убывает.
–В. Функция y = 5cos x не имеет наибольшего значения.
+Г. Функция y = cos 3x + 2
имеет период 
.
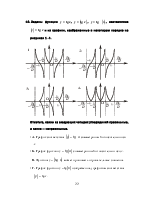
9. На рисунках 1 и 2 изображены графики функций, которые связаны с функцией y = tg x.
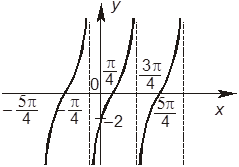
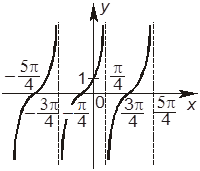
Рис. 1 Рис. 2
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. На рисунке 1
изображен график функции y = 2tg
.
–Б. На рисунке 1 изображен
график функции y = tg
.
+В. На рисунке 2 изображен график функции y = tg
.
–Г. На рисунке 2 изображен график функции y = 2tg .
10. Задана
функция y = 
.
Отметьте, какие из следующих четырех утверждений правильные, а какие —
неправильные.
–А. Область определения этой
функции: x ¹ 
; kÎZ.
–Б. Множеством значений этой функции являются все отрицательные числа.
–В. Заданная функция нечетная.
–Г. Заданная функция четная.
11. Отметьте, какие из следующих четырех утверждений относительно периодичности тригонометрических функций правильные, а какие — неправильные.
–А. Периодическая функция f(x) может иметь область определения х ³ 0.
–Б. Функция y = sin 
периодическая.
+В. Если функция f1(x) периодическая с периодом Т, а функция f2(x) периодическая с периодом 2Т, причем функции f1(x) и f2(x) имеют общую область определения, то функция f (x) = f1(x) + f2(x) всегда будет периодической с периодом 2Т.
+Г. Функция y = соs х + tg
периодическая с периодом 4p.
12. Заданы функции y = sin x, y = 
, y = sin 
,
соответствие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.