Алгебра 10 класс. Тема: Основные тригонометрические формулы
Цель данного теста — проверить, умеет ли учащийся:
¾ пользоваться соотношениями между тригонометрическими функциями одного аргумента (с учетом знаков функций в соответствующей четверти);
¾ пользоваться формулами сложения тригонометрических функций;
¾ пользоваться формулами двойного и половинного аргумента;
¾ пользоваться формулами приведения;
¾ пользоваться формулами преобразования суммы тригонометрических функций в произведение и преобразования произведения тригонометрических функций в сумму (соответствующие формулы приведены в справочном материале на с. 79).
Вариант 1
Записывая ответы на задания теста, обведите буквы, отвечающие
утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям,
которые вы считаете неправильными. Например, если вы считаете правильными
утверждения А и В, а неправильными — утверждения Б и Г, запишите 
. Если хотя бы одна буква из
4-х будет не отмечена, задание считается невыполненным.
1. На единичной окружности задана точка М, которую получили поворотом точки А на угол a (см. рисунок).
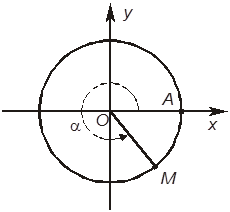
Выберите правильное утверждение.
–А. Точка М находится в первой четверти.
+Б. sin a — ордината точки М.
–В. sin a — абсцисса точки М.
–Г. Для угла a, заданного на рисунке, sin a > 0.
2. Пользуясь соотношением sin2 a + cos2 a = 1, выберите правильное утверждение.
–А. sin2 
+ cos2 > 1.
–Б. 
= 
.
–В. sin2 30° + cos2 30° < 1.
+Г. sin2 15° = 1 – cos2 15°.
3. Выберите правильное значение выражения
–2sin 15° cos 15°,
пользуясь формулой синуса двойного угла:
sin 2a = 2sin a cos a
и значением sin 30° = 
.
|
–А. |
–Б.
– |
–В. |
+Г.
– |
4. Дано: sin a = 
,
где 
< a < p.
Учитывая знак косинуса в соответствующей четверти и
пользуясь формулой cos2 a = 1 – sin2 a, отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. cos2 a = 
.
–Б. Угол a находится в третьей четверти.
+В. cos a — отрицательное число.
–Г. cos a = 
.
5. Чтобы вычислить sin 75°, воспользовались тем, что
sin 30° = , cos 30° = 
, sin 45° = cos 45° = 
и формулой
sin (a + b) = sin a cos b + cos a sin b.
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. 75°=30°+45°.
–Б. sin75°=
.
+В. sin75°=
.
–Г. sin75°=
.
6. Дано
выражение: 
.
Для преобразования числителя воспользовались формулой
sin a – sin b = 2sin 
cos 
.
Отметьте, какие из выражений А–Г можно получить после упрощения заданного выражения, а какие — нельзя.
|
–А. 2sin 3a. |
+Б. 2sin 2a. |
–В. 2cos 3a. |
–Г. cos 2a. |
7. Известно, что tg a = – 
, где 0 <
a <
p. Отметьте, какие из следующих четырех утверждений правильные, а
какие — неправильные.
–А. Угол a находится в первой четверти.
+Б. cos a = – .
+В. sin a = 
.
+Г. ctg a = – 
.
8. Пользуясь формулами приведения, отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. sin (90° + a) = cos a.
–Б. cos (p – a) = cos a.
+В. tg (90° + 45°) = – ctg 45°.
–Г. ctg (p + 3) = – ctg 3.
9. Отметьте, какие из выражений можно получить после упрощения выражения 
,
а какие — нельзя.
–А. ctg 2a.
+Б. tg 2a.
–В. 
.
+Г. 
.
10. Задано
выражение 
, причем известно, что tg a = 5. Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Из равенства tg a = 5 можно получить равенство sin a = 5cos a.
–Б. Если
числитель и знаменатель заданного выражения разделить на cos a
¹ 0,
то можно получить выражение 
.
–В. Значение заданного
выражения равно 
.
+Г. Значение заданного
выражения равно 
.
11. Задано
выражение 
, где < a < p. Отметьте,
какие из приведенных ниже выражений можно получить в результате преобразования
заданного выражения, а какие — нельзя.
–А. tg a.
–Б. ctg a.
+В. 
.
+Г. – сtg a.
12. Задано выражение аsin a + bcos a, где а ¹ 0, b ¹ 0. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Заданное выражение можно
представить в виде
.
+Б. Существует такое
число j, что одновременно выполняются
равенства: соs j = 
, sin j = 
.
–В. Заданное выражение можно
представить в виде 
sin(a – j),
где соs
j = 
, sin j = 
.
+Г. 
£ .
Вариант 2
Записывая ответы на задания теста, обведите буквы, отвечающие
утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие
утверждениям, которые вы считаете неправильными. Например, если вы считаете
правильными утверждения А и В, а неправильными — утверждения Б и Г,
запишите . Если хотя бы одна буква из
4-х будет не отмечена, задание считается невыполненным.
1. На единичной окружности задана точка М, которую получили поворотом точки А на угол a (см. рисунок). Выберите правильное утверждение.
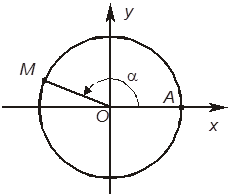
–А. Точка М находится в третьей четверти.
–Б. cos a — ордината точки М.
+В. cos a — абсцисса точки М.
–Г. Для угла a, заданного на рисунке, cos a > 0.
2. Пользуясь соотношением 1 + tg2
a = 
, выберите правильное
утверждение.
–А. 1 + tg2 15° = 
.
+Б. tg2 40° = 
– 1.
–В. 1 + tg2
= 
.
–Г. tg2 25° = 
.
3. Укажите правильное значение выражения
cos2 15° – sin2 15°,
пользуясь формулой косинуса двойного угла
сos2a = cos2 a – sin2 a
и значением соs 30° = .
|
–А. |
–Б. – |
+В. |
–Г. – |
4. Дано: cos a = 
, где 
< a < 2p. Учитывая знак синуса в соответствующей четверти и
пользуясь формулой sin2 a = 1 – cos2 a, отметьте, какие из следующих четырех утверждений правильные, а какие —
неправильные.
+А. sin2 a = 
.
+Б. Угол a находится в четвертой четверти.
–В. sin a — положительное число.
–Г. sin a = .
5. Чтобы вычислить cos 75°, использовали то, что
sin 30° = , cos 30° = , sin 45° = cos 45° =
и формулой
cos (a + b) = cos a cos b – sin a sin b.
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. 75°=30°+45°.
–Б. cos75°=
.
–В. cos75°=
.
+Г. cos75°=
.
6. Дано выражение: 
.
Для преобразования числителя воспользовались формулой
sin a + sin b = 2sin cos .
Отметьте, какие из выражений А–Г можно получить после упрощения заданного выражения, а какие — нельзя.
|
+А. 2sin 4a. |
–Б. 2sin 3a. |
–В. sin 4a |
–Г. сos 3a. |
7. Известно, что сtg a = ,
где p <
a <
2p.
Отметьте, какие из следующих четырех
утверждений правильные, а какие — неправильные.
+А. Угол a находится в третьей четверти.
–Б. cos a = .
+В. sin a = – .
–Г. tg a = – .
8. Пользуясь формулами приведения, отметьте, какие из следующих четырех
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
.