Булевы предикаты замкнутых областей. R-отображения и R-предикаты. Основные системы R-функций, страница 3

Таблица 1

Таблица знаков R-функции f(x)=x₁x₂ и таблица истинности сопровождающей булевой функции

Булева функция F(x), образующая вместе с R-функцией f(x) коммутативную диаграмму (см. рисунок 3), называется сопровождающей булевой функцией.

Итак, R-предикат области – это функция, которая положительна внутри области и отрицательна за её пределами.  В случае непрерывной функции на границе она получается равной нулю.  Для построения R-предиката сложной области по R-предикатам опорных областей надо построить такую действительную функцию, чтобы её знак определялся знаками аргументов, причём таблица знаков R-функции должна совпадать с таблицей истинности сопровождающей булевой функции.

В.Л.Рвачёвым доказаны теоремы об основных свойствах R-функций. В частности, установлено, что множество R-отображений и множество сопровождающих функций замкнуты (т.е. любая суперпозиция R-функций является R-функцией). Кроме того, установлено, что одна и та же булева функция может оказаться сопровождающей для различных R-отображений. Если считать, что различные R-отображения, имеющие общую сопровождающую булеву функцию, эквивалентны, то всё множество R-отображений можно разбить на ветви эквивалентных функций. Введём также понятие достаточной полноты системы R-функций, состоящее в существовании R-функций в каждой ветви множества сопровождающих функций.

3. Основные системы R-функций

Рассмотрим теперь, как получить R-функцию, если сопровождающая булева функция известна. Основное пространство для построения R-отображений – числовая ось R¹. Будем рассматривать действительные функции, определенные на всей числовой оси.

Приведём некоторые их свойства.

1.  Для любого разбиения числовой оси функция y = C = const является R-функцией. Сопровождающей функцией для неё будет булев предикат той части числовой оси, которой принадлежит константа С.

2.  Для любого разбиения числовой оси функция y = х является R-функцией. К числу сопровождающих функций принадлежит функция k-значной логики , i=1, …, k.

3.  Пусть разбиение числовой оси симметрично относительно начала координат. Тогда функция  y = -х является R-функцией с сопровождающей .

4.  Для любого монотонного разбиения числовой оси функции  и  будут R-функциями. В частности, для биекции числовой оси сопровождающими функциями будут функции двузначной логики; нетрудно проверить, что булева конъюнкция будет сопровождающей для функции , а дизъюнкция – для . Доказательство этого факта в случае разбиения числовой оси на положительную и отрицательную части основывается на сопоставлении таблиц истинности сопровождающих функций с таблицами знаков R-функций.

В дальнейшем внимание будет уделяться R-функциям, соответствующим биекции (2). Даже и в этом частном случае можно построить множество систем R-функций, сопровождающими для которых будут основные функции двузначной логики. Некоторые из этих систем приведены в таблице 2.

Таблица 2

Основные системы R-функций

Система R_a, приведенная в таблице 2, содержит параметр a, который может принимать значения из интервала (-1, 1). Этот параметр, вообще говоря, может быть функцией координат. Представляют интерес частные случаи: R₀ при a=0 и R₁ при a=1. Функции из этих систем приведены ниже.

Для a=0:

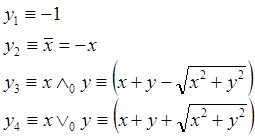
Для при a=1:

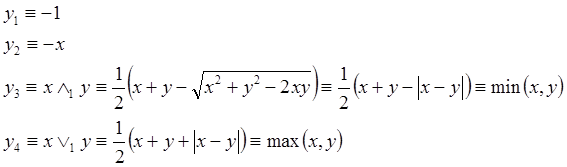
Недостатком этих систем является недифференцируемость в начале координат, а функций системы R₁ – и на биссектрисе первого и третьего координатных углов.  Система R^m₀, приведенная в таблице 2, состоит из функций класса C^m.

Доказательство того, что знаки этих функций однозначно определяются знаками аргументов, и выяснение таблиц знаков функций рекомендуется проделать самостоятельно.