Булевы предикаты замкнутых областей. R-отображения и R-предикаты. Основные системы R-функций, страница 2

Такая функция называется двузначным булевым предикатом множества. Принадлежность точки множеству можно теперь установить по значению булева предиката множества в данной точке. Очевидно, что, если мы имеем булевы предикаты опорных множеств, то предикаты производных множеств можно вычислить с помощью операций булевой алгебры.

Замечание. При использовании двузначных булевых предикатов мы не различаем внутренних и граничных точек множеств. Это не всегда удобно. Используя трёхзначную булеву алгебру, можно было бы ввести трёхзначный предикат, принимающий, например, значение 2 внутри области, 1 – на её границе и 0 вне области. Однако в дальнейшем мы не будем пользоваться трёхзначными предикатами, а вопрос о границах будем рассматривать отдельно в каждом случае.

Покажем, как с помощью булевых операций построить предикат области, изображённой на рисунке 2.

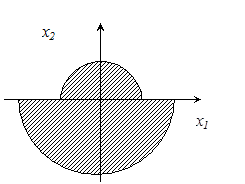
Рисунок 2. Область, составленная из двух полукругов.

Запишем предикаты опорных областей:

круг малого радиуса r: S₁(x) = ;

круг большого радиуса: S₂(x) = ;

верхняя полуплоскость: S₃(x) = .

Тогда булева функция S(x) =  принимает значение 1 в точках изображённой на рисунке 2 фигуры.

Булев предикат можно построить и для областей размерности, не равной двум. В общем случае булев предикат n-мерной области – это отображение вида , ставящее в соответствие каждому набору n координат одно из двух булевых значений.

В частности, размерность n может быть равна и единице. Булев предикат :

                                                                                                    (2)

задаёт биекцию числовой оси на положительную и отрицательную полуось. Предикатное уравнение S₂(x)=1можно рассматривать как уравнение положительной полуоси. Применив у нему операцию отрицания, получим булев предикат отрицательной полуоси. (Здесь опять возникает вопрос о граничной точке, который в рамках двузначной булевой алгебры не решается: строго говоря, уравнение  задаёт открытое множество, не включающее точку x=0).

Итак, подведём итоги.

Построение предикатного уравнения заданного геометрического объекта связано с анализом формирования этого объекта из других, более простых опорных объектов. Булева функция предикатов опорных объектов чаще всего бывает не задана и должна строиться по виду данного геометрического объекта. Затруднений здесь обычно не возникает, поскольку сам вид объекта подсказывает, какие объекты следует выбрать в качество опорных и какие операции над опорными множествами следует проделать, чтобы получить заданный объект. Переход от операций над множествами к операциям над их предикатами достаточно тривиален; аналогии между этими операциями легко установить, если усвоен базовый курс дискретной математики.

В то же время мы ещё не приблизились к тому, чтобы составить такие уравнения объекта, какие изучаются в аналитической геометрии, в которых бы использовались только обычные операции над действительными числами.

2. R-отображения и R-предикаты

Вернёмся ещё раз к задачи биекции числовой прямой. Формула (2) задаёт булев предикат положительной полуоси и является отображением . Можно было бы попытаться определить некоторую действительную функцию точки, знак которой определял бы принадлежность точки заданному множеству. аналогично тому, как знак переменной x  определяет принадлежность точки в R¹ правой полуоси. Такую функцию естественно назвать R-предикатом точечного множества.

Для построения R-предикатов сложных объектов из R-предикатов опорных областей понадобятся функции, знак которых однозначно определяется сочетанием знаков аргументов. Такие функции называются R-функциями.

Сформулируем это определение более строго.

Определение. Отображение называется R-отображением, если существует такая функция k-значной логики , что композиция тождественно равна композиции .

Этому определению можно придать наглядность с помощью следующей диаграммы (рисунок 3).

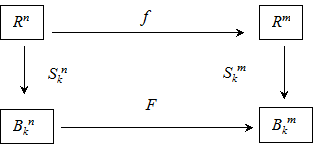
Рисунок 3.  Коммутативная диаграмма R-отображения.

Область в Rⁿ образована базовыми областями, булевы предикаты которых  являются аргументами булевой функции F - m-мерного k-значного предиката составной области. С другой стороны, действительная функция f отображает Rⁿ в пространство меньшей размерности m так, что выбранная биекция числовой оси опять даёт тот же самый предикат.

Рассмотри пример, иллюстрирующий понятие R-отображения.

Пусть область W задана неравенством: . Ту же самую область можно задать с помощью булевой функции двух булевых предикатов опорных областей – верхней полуплоскости  и правой полуплоскости , если положить . Нетрудно проверить, что таблица истинности этой функции совпадает с таблицей знаков функции f(x) (таблица 1). Таким образом, рассматривая x₁ и x₂ как R-предикаты полуплоскостей, мы имеем R-отображение f(x), которая положительна в тех точках, где булев предикат F(x) равен единице, и отрицательна, где булев предикат равен нулю (граничные точки по-прежнему не рассматриваем).