Высказывания. Свойства операций над высказываниями. Основные методы построения полиномов Жегалкина

Аналогично предыдущему доказывается замкнутость класса . в) Пусть , где  самодвойственные функции. Тогда , т. е. . . Следовательно, класс  замкнут. г)Пусть , где . Покажем, что . Пусть    Наборы переменных состоят из переменных, встречающихся у функций   соответственно.  Возьмем два набора  и  значений переменных . Они определяют наборы  значений переменных  причем . Так как , то

.

Тогда . Функция , поэтому  . Отсюда

Следовательно, класс  замкнут. д) Класс  замкнут, так как линейное выражение, составленное из линейных выражений, является линейным.

(13)

Лемма (о несамодвойственной функции). Если, то из нее путем подстановки функций  и  вместо можно получить несамодвойственную функцию одного переменного, т.е. константу. Доказательство. Так как , то существует набор  такой, что  .

Рассмотрим функцию . Пусть

. Тогда

Следовательно, константа 0 или 1.

Замечание. Если , то вместо  подставляем , если же  то . Замечание. Для того чтобы определить, является ли функция , заданная своим вектором значений, самодвойственной,  следует проверить, получается ли вторая половина вектора из первой отражением и последующим инвертированием его координат.

Лемма (о немонотонной функции). Если , то подстановкой констант ,  и функции  из нее можно получить . Доказательство. Если , то найдутся два набора значений переменных  и  такие, что  и . Поскольку наборы  и  различаются в  координатах (), то, меняя по одной координате, между ними можно вставить  соседних наборов, т.е. таких, что

и каждый следующий набор получается из предыдущего изменением ровно одной координаты. Так как , то в этой цепочке найдутся два соседних набора переменных  и  такие, что  и . Пусть эти наборы различаются в - ой координате:

 .

Рассмотрим функцию

.

Имеем

Поскольку, , то . Замечание. Для проверки на монотонность функции , заданной своим вектором значений, нужно сначала разделить его две равные части  и . Если соотношение  не выполнено, то  немонотонная. В противном случае разделим каждый из полученных векторов опять пополам  и . Проверим сначала первую пару на выполнение соотношения , и в случае положительного результата вторую. Если хотя бы для одной пары соотношение не выполняется, то функция немонотонная. В противном случае этот алгоритм продолжаем дальше.

(14)

Лемма (о нелинейной функции). Если , то из нее путем подстановки констант ,  и функций  и , а также, быть может, инвертированием , можно получить функцию . Доказательство. Возьмем полином Жегалкина для :

.

В силу нелинейности полинома в нем найдется член, содержащий не менее двух множителей. Без ограничения общности можно считать, что среди этих множителей присутствуют  и . Тогда можно преобразовать полином следующим образом:

где в силу единственности полинома .

Пусть  таковы, что . Тогда

где  – константы, равные  или . Рассмотрим функцию , получаемую из  следующим образом:

.

Очевидно, что

 .

Следовательно, .

(15)

Теорема Поста (о полноте). Для того чтобы система функций  была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов . Доказательство. Необходимость. Пусть система  полна. Тогда . Допустим, что  содержится целиком в каком-либо из классов Поста (обозначим его через ), т.е. . В этом случае . Отсюда , что невозможно. Достаточность. Пусть  не содержится целиком ни в одном из пяти классов Поста. Выделим из нее подсистему функций. , где , и на ее основе построим полную систему.

1. При помощи  построим функции (константы) 0 и 1 или функцию .  Разберем отдельно два случая:

(а) ;(б) .

(а) Рассмотрим функцию . Из цепочки равенств  следует, что .

(б) В этом случае для функции  получаем , т.е. . Аналогичным образом, используя функцию , строим константу 0 или функцию .  Итак, нами построены либо функция , либо обе константы 0 и 1. или  2. Если построена , то с помощью  и , применяя лемму о несамодвойственной функции, строим константы 0 и 1. Если есть обе константы 0 и 1, то .с помощью функций 0, 1 и , используя лемму о немонотонной функции, можно построить .

3. При помощи 0, 1,  и , применяя лемму о нелинейной функции, строим функцию . Система полная. Значит, и  полная. Отсюда следует полнота системы . Теорема доказана.  Следствие 1. Из всякой полной системы можно выделить полную подсистему, содержащую не более пяти функций.

(16)

Каждой бинарной операции в алгебре логики соответствует функциональный элемент с двумя входами и одним выходом, унарной – с одним входом и одним выходом (см. рис. 1.7). Если набор функциональных элементов (ФЭ) соответствует полной системе в , то любую булеву функцию можно выразить формулой через функции полной системы и реализовать ее с помощью соответствующих ФЭ. Логическая схема , выходные сигналы  которой описываются системой булевых функций , где  входные сигналы логической схемы (, ), называется схемой из функциональных элементов (СФЭ).

Теорема. Для того, чтобы для произвольной системы 

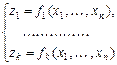 существовала схема  из ФЭ с  входами  и  выходами  необходимо и достаточно, чтобы набор ФЭ соответствовал полной системе функций.

Обычно для построения схем используются базис  (этот базис называется стандартным или булевым) или  (базис Жегалкина). Обозначим через  функционал, равный числу элементов в схеме , означающий