Для построения линии влияния изгибающего момента в сечении удаляется связь, препятствующая взаимному повороту близко расположенных друг от друга соседних сечений, т. е. между этими сечениями вводится цилиндрический шарнир.
Построение линии влияния поперечной силы в сечении предшествует удаление связи, препятствующей взаимному перемещению близко расположенных друг от друга соседних сечений в направлении перпендикулярном оси балки, т. е. введение между этими сечениями поступательного шарнира, а линии влияния реакции вертикальной шарнирно подвижной опоры – удаление связи препятствующей взаимному перемещению точек в вертикальном направлении.
Действие отброшенной связи заменяется положительным усилием Х. В образовавшемся после удаления связи механизме с одной степенью свободы с помощью теоремы о трёх мгновенных центрах вращения определяются необходимые относительные и абсолютные центры вращения дисков. Механизму задают возможные перемещения по направлению положительного усилия Х и получают эпюру перемещений δF сечений балки в направлении единичной сосредоточенной силы. В соответствии с принципом возможных перемещений линия влияния усилия совпадает с эпюрой перемещений, если ординаты этой эпюры измерить в масштабе δх = 1, т. е. в масштабе перемещения по направлению усилия Х. Зная этот масштаб и учитывая линейность эпюр возможных перемещений отдельных дисков механизма, определим необходимые ординаты линии влияния усилия Х из геометрических соображений. Так как возможные перемещения механизму заданы в направлении положительного усилия Х, знак линии влияния этого усилия выше оси отсчёта будет положительным, а ниже – отрицательным.
Значение любой величины от заданной нагрузки может быть определено с помощью её линии влияния. Влияние различного рода нагрузок (сосредоточенных сил, сосредоточенных моментов, распределённых по какому-либо закону нагрузок, в том числе и равномерно распределённых) на исследуемую величину определяется правилами загружения линий влияния.
1.4 Объемлющие эпюры внутренних усилий
Объемлющий эпюрой какой-либо величины (например, изгибающего момента в определённом сечении) называется график изменения этого усилия вдоль оси рассматриваемого элемента сооружения, ординаты которого представляют собой его максимальные и минимальные значения при самом невыгодном сочетании постоянных и временных нагрузок.
В индивидуальном расчётном задании, заданная нагрузка является постоянной, а «поезд», состоящий из ряда сосредоточенных сил, перемещающийся по балке в любом направлении и занимающий на ней любое положение – временной.
При наличии подвижной временной нагрузки определение ординат и построение объемлющих эпюр внутренних усилий производится в следующем порядке:
1. Строится эпюра интересующего нас внутреннего усилия от постоянной нагрузки (в нашем задании – эпюра изгибающих моментов).
2. Для сечений, в которых определяются ординаты объемлющей эпюры, строятся линии влияния соответствующего внутреннего усилия.
3. Определяются критические положения заданного «поезда» отдельно над положительными и отрицательными участками построенных линий влияния и путём загружения их сосредоточенными силами вычисляются максимально возможные положительные и отрицательные значения рассматриваемого внутреннего усилия. В случае треугольного и полигонального очертания линий влияния критический груз, соответствующий критическому положения «поезда» устанавливается методом попыток (поочерёдной установкой сосредоточенных грузов «поезда» над вершинами линий влияния) ил графическим способом.
4.Вычисляются в табличной форме ординаты объемлющей эпюры интересующего нас внутреннего усилия.
Постановка задачи
Для многопролётной балки (рис.1) необходимо:
1. Произвести кинематический анализ и построить её рабочую схему;
2. Построить эпюры изгибающих моментов и поперечных сил от нагрузки;
3. Построить линии влияния изгибающих моментов и поперечных сил в сечениях 1 и 2 балки, а также линию влияния наибольшей по абсолютной величине реакции вертикальной опорной связи;
4. Загружением вышеперечисленных линий влияния заданной нагрузкой определить изгибающие моменты и поперечные силы в сечениях 1 и 2 балки, а также значение наибольшей по абсолютной величине реакции вертикальной опорной связи. Сопоставить величины, найденные путём загружения линий влияния, с соответствующими значениями, полученными при построении эпюр внутренних усилий.
5. На участке балки, показанном пунктирной линией, построить объемлющую эпюру изгибающих моментов, вычислить её ординаты через 0,5а.
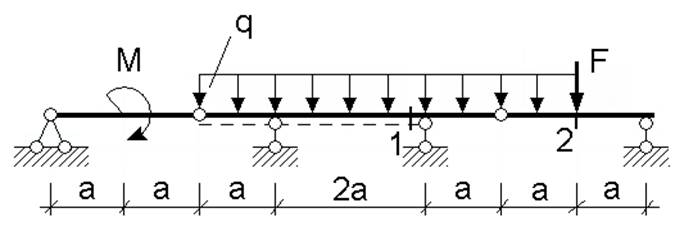
Дано:
M = 10 кН м
q = 3 кН/м
F = 8 кН
a = 2,5 м
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.