Квантованное электромагнитное поле и переходы в квантовых системах

Квантованное электромагнитное поле и переходы в квантовых системах.

1.  Инвариантная теория возмущений.

Рассмотрим переходы, которые происходят под действием переменного возмущения. Гамильтониан системы представим в виде

      ,                                                                 (1.1)

где  - часть гамильтониана системы, независящая от времени,  - зависящая от времени часть гамильтониана. Строго говоря, явная зависимость от времени связана с неполным квантовым описанием системы. Например, зависящее от времени внешнее классическое поле. При последовательном квантовом описании явная зависимость от времени отсутствует. Оператор   может не зависеть явно от времени. Это часть гамильтониана, которую выделили во взаимодействие -. В последовательной квантовой теории оператор Гамильтона не зависит явно от времени -.  Явная зависимость от времени обусловлена непоследовательностью в описании квантовой системы. Например, рассматриваются внешние, классические, поля, которые зависят от времени. 

Осуществив замену волновой функции

, перейдем в представление взаимодействия. Волновая функция состояния в представлении взаимодействия удовлетворяет уравнению

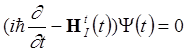   ,                                                               (1.2)

где часть гамильтониана, отвечающая за взаимодействие, приобретает следующую дополнительную зависимость от времени (дополнительную к явной зависимости от времени)

.

Операторы в данном представлении приобретают такую же дополнительную зависимость от времени

.

Эта дополнительная зависимость от времени аналогична динамической зависимости от времени физических величин через зависимость последних от обобщенных координат и обобщенных импульсов. В последовательной классической механике функция Гамильтона тоже не зависела явно от времени. Явная зависимость от времени в классической механике была обусловлена зависимостью от времени связей, наложенных на систему. Аналогом связей являются классические поля, наложенные на квантовую систему.

Волновую функцию через малый промежуток времени dt можно найти следующим образом

.

После многократного повторения предыдущей операции решение уравнения  (1.2) можно представить в следующем виде

     ,                            (1.3)

где индексы  f  и i  отмечают конечное и начальное состояния, - бесконечно малые приращения времени, которые последовательно заполняют отрезок времени от начала до конца процесса. Произведение экспонент не сводится к экспоненте, в показателе которой сумма показателей отдельных экспонент в произведении, так как операторы в разные моменты времени не обязаны коммутировать друг с другом. Это произведение можно записать в символическом виде

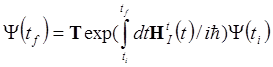 .                                  (1.4)

Символ T - хронологический оператор, который расставляет операторы в хронологической последовательности убывания времен. В задачах рассеяния обычно начальное время минус бесконечность, конечное плюс бесконечность (такое приближение вполне обосновано тем, что обычно время измерения значительно превосходит время характерное для квантовых процессов):    

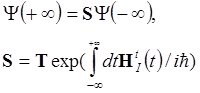                                                          (1.5)

в подробной символической записи

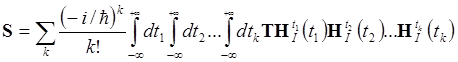    (1.5’)

и в виде пригодном для непосредственного счета

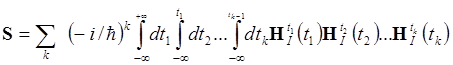 .   (1.5’’)

В первом приближении:

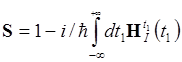
во втором приближении:

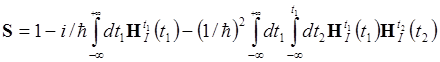
2. Вероятность перехода и S- матрица.

Рассмотрим переход из начального состояния i в конечное состояние f за время (время измерения) значительно большее характерного времени микроскопических процессов. В конечном и начальном состояниях возмущение отсутствует. Его включение и выключение можно осуществить адиабатически (медленно). Гамильтонов оператор взаимодействия не зависит явно от времени,  кроме зависимости от времени, которая обеспечивает включение и выключение взаимодействия. Переходы из начального состояния  i  в конечное состояние f  полностью описываются заданием S-матрицы рассеяния  (1.5):

 ,                                                                                               (2.1)

где  - вектор конечного состояния (волновая функция),  - вектор начального состояния,  - матричные элементы S-матрицы рассеяния:

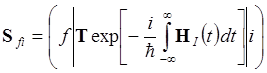,                                                      (2.2)           где    - гамильтониан взаимодействия, которое вызывает переходы в квантовой системе, не зависит явно от времени. Конечное и начальное  состояние являются собственными состояниями гамильтониана  с собственными значениями  . 

Преобразуем   S-матрицу (1.15’’). Учтем адиабатичность включения и выключения возмущения добавлением   в гамильтонов оператор взаимодействия (во время процессов перехода системы из одного состояния в другое эта добавка равна единице):

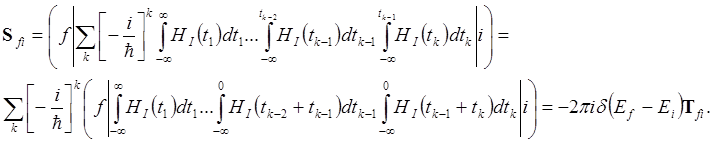
(2.3)

где ввели T-матрицу рассеяния.  После взятия интегралов по времени:

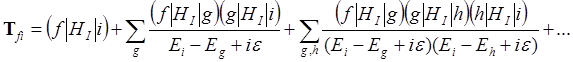               (2.4)

где учли то, что начальное и конечное состояния являются собственными состояниями  и

, что      .

Соотношение (2.4) можно записать в операторном  виде

.

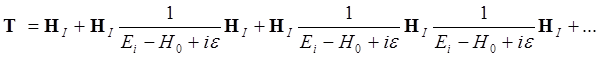Легко видеть, что после выноса за скобку 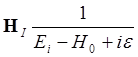, начиная со второго слагаемого в правой части, получим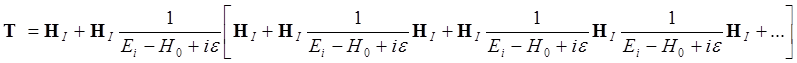

После суммирования ряда в скобках имеем операторное уравнение

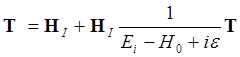                     ,                                           (2.5)

которое можно представить в матричном виде

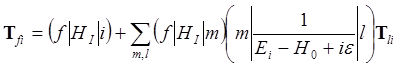            .                     (2.6)

Вероятность перехода из начального состояния  i в конечное состояние f можно представить в виде (в силу нормированности волновых функций)

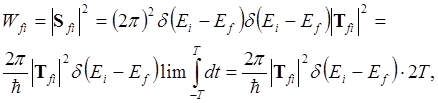
где 2T – время измерения. Дельта- функция выражает закон сохранения энергии на больших временах измерений. В эксперименте наблюдается не вероятность перехода, а вероятность перехода в единицу времени

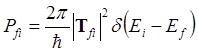.                                                                      (2.7)

Таким образом  вероятность перехода полностью определяется матрицей рассеяния (2.6).