Состояние и измерение в квантовой и классической физике, страница 4

, при рассеянии на p/2  имеем

.

Этот результат вполне естественен. Так как в эксперименте проявляются квадраты модулей амплитуд, то знак при амплитуде не может проявиться. Изначально возможны оба варианта сложения и вычитания амплитуд. Природа сделала выбор: существует два типа частиц. Сложение амплитуд для бозонов. Вычитание амплитуд для фермионов. Это проявляется том, что для бозонов вероятность рассеяться в состояние, где есть бозоны больше чем в состояние, где нет бозонов. Именно поэтому есть сверхтекучесть, сверхпроводимость и лазеры. Бозоны осуществляют взаимодействие между частицами вещества, которые являются фермионами.  Для фермионов есть запрет на рассеяние в состояние, в котором уже есть фермион – принцип запрета Паули. Следствие многообразие атомов и молекул, в конечном итоге многообразие мира.

Принцип суперпозиции для квантовых состояний: если состояния (процессы) неразличимы, то амплитуда складываются для бозонов и вычитаются для фермионов, если состояния (процессы) различимы, то складываются вероятности.

8. Феймановское суммирование по всем возможным траекториям.

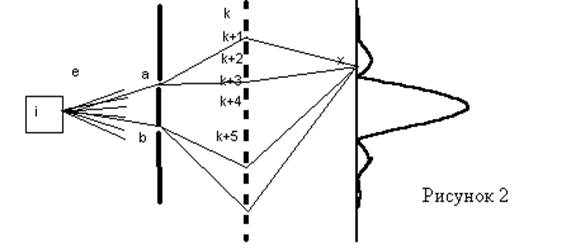
Рассмотрим рассеяние электрона на двух щелях:

Переход электрона из i в  a  может осуществляться различными способами. Рассмотрим один из них. Электрон из i попадает в a . Этот процесс  описывается амплитудой

Далее из a   в k+3 амплитудой 

Так как эти события независимые (при рассмотрении только одного варианта перехода), амплитуды необходимо перемножить для получения амплитуда перехода из i  в k+3

Далее переход из k+3 в  x с амплитудой

Окончательно:

.

Амплитуда перехода электрона из источника i  на фотопластинку x - сумма всех возможных амплитуд (не разность, так как здесь рассматривается один электрон, а путей у него много, складываются амплитуды возможных переходов для одного электрона. Если рассматривать амплитуды перехода для двух электронов, то  они будут вычитаться). Амплитуда перехода из  i в x через b и k получается следующим образом:

.

Амплитуда перехода из i в x  всеми способами:

.

Вероятность перехода есть

.

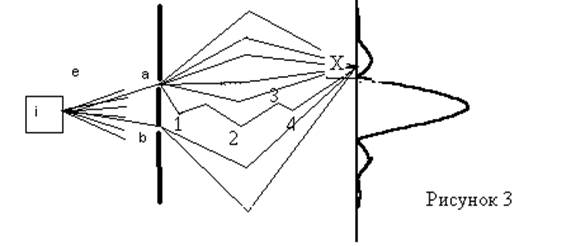
Если щели во втором экране достаточно велики, то наличие этого экрана или отсутствие не скажется на рассеянии электронов на первом экране:  . Если закрыть хотя бы одну щель во втором экране, результат рассеяния при наличии второго экрана будет отличаться от рассеяния без второго экрана.

Амплитуда перехода по пути :

.

Если в точках на траектории происходит взаимодействие квантовой системы, то за каждую остановку необходимо уплатить множителем   :

Амплитуда перехода квантовой системы из одного состояния в другое есть сумма амплитуд перехода по всем возможным  траекториям. Амплитуда перехода на траектории есть произведение амплитуд перехода на участках траектории с соответствующим множителем за каждую остановку.

Литература.

1.  В.А. Фок Квантовая физика и строение материи. ЛГУ., 1965

2.  В.А. Фок Начала квантовой механики. Наука. 1976

3.  Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. Т. 8,9. Мир, Москва (1978)

4.  В.П. Крайнов Взаимосвязь между квантовой и классической физикой. Соросовский образовательный журнал. №4. 1998

5.  Р. Фейнман КЭД странная теория света и вещества. Москва. Наука,1988. (Квант, Вып. 66)