Состояние и измерение в квантовой и классической физике, страница 3

6. Квантовое состояние системы и амплитуда вероятности.

Формирование квантового состояния включает приготовление системы и создание внешних условий – начальный опыт (пучек электронов, пучек электронов прошедший через кристалл, набор атомов в определенных условиях). Вторая стадия – поверочный опыт -взаимодействие с прибором. Вместе – завершенный опыт. Начальный опыт можем воспроизвести многократно. Проводим измерения прибором. Наблюдаем статистику измерений, вероятности тех или иных реализаций, которую и должны предсказать в теории. Совокупность потенциальных вероятностей для поверочного опыта, при определенном начальном опыте, рассматривается как характеристика состояния квантовой системы. Максимально полная характеристика системы – просто состояние системы. Развитие потенциальных возможностей во времени (измерений в различные моменты времени над системой) – развитие во времени состояния.

Состояние системы характеризуется амплитудой вероятности или волновой функцией:

, где x - характеризует конечное состояние, a -характеризует начальное состояние, начальный опыт. Квадрат модуля амплитуды вероятности – вероятность обнаружить систему в состоянии

вероятность найти в x , если сформировали состояние  в условиях a. Это и означает, что задали совокупность потенциальных возможностей. Почему ввели амплитуду, а не пользуемся вероятностями, которые проверяются в эксперименте? Вероятности для конкретного измерения величины х при условиях а. Амплитуду можно преобразовать и посмотреть на систему с другой стороны, например, узнать потенциальные возможности наблюдения величины у при условии а или изменить начальные условия.

Прибор на языке математики – оператор, который действует на волновую функцию, правило по которому трансформируется волновая функция:

, под воздействием прибора получаем новую волновую функцию, которая зависит от начальных условий (a)  и прибора (А). Если в результате воздействия прибора волновая функция умножается на число, то имеем собственное состояние для данного прибора, которое отмечаем значением измеренной величины:

.        

7. Тождественные частицы и принцип суперпозиции состояний.

Что делать с амплитудами? Рассмотрим рассеяние  фльфа-частицы на ионе кислорода:

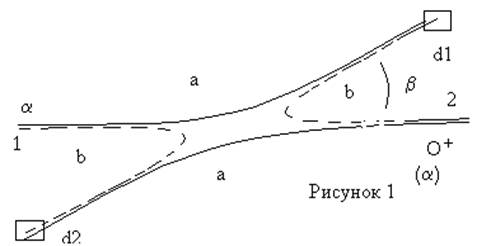Возможны два процесса а) и в). Амплитуда перехода из 1 в d2:  f(b)=  из 1 в d1 : f(p-b)=. Вероятность обнаружить какую либо частицу в детекторе d1 есть:

Если в этом опыте заменить ион кислорода на другую альфа-частицу (⁴He), то результат эксперимента изменится (если заменить на ³He, то не изменится качественно). Причиной изменения станет принципиальная неразличимость рассеивающихся частиц. Которая из них рассеялась на  угол b ,  а которая на угол p-b, мы не можем ответить. Согласуется с экспериментом по рассеянию альфа-частиц расчет, в котором вероятность рассеяния рассчитывается по формуле

что означает что амплитуда перехода, который может происходить различными неразличимыми  физически путями, получается сложением амплитуд неразличимых процессов. В частности вероятность рассеяния на p/2  для неразличимых частиц в два раза больше чем вероятность рассеяния на p/2 для различимых частиц:

Различимые:       , неразличимые:    .

Но, если мы проведем этот эксперимент с поляризованными электронами (с определенной проекцией спина), то получим совершенно неожиданный результат рассеяние на p/2 отсутствует. Это можно объяснить только тем, что амплитуды неразличимых процессов могут и вычитаться: