Проведение нагрузочных испытаний тепловозов, страница 2

n_г- скорость вращения якоря, с^-1.

С другой стороны,  можно записать следующую простую зависимость:

Er=C_erB_б,U_r      (2.3) Где C_er⁼pNatl/a - магнитная постоянная ТГ.

Значение индуктивности в воздушном зазоре определяется по характеристике холостого хода или по кривой намагничивания ^

Где Fi - результирующая н.с. обмотки возбуждения ТГ.

Генератор    ГП311Б,    несмотря    на    размер,    обладает значительной величиной реакции якоря. Для любого режима его работы справедливо следующее уравнение результирующей н.с:                               

                             F=F_B+F_A,        (2.4)

 Где F_AF_B - н.с. - обмотки возбуждения и реакции якоря.

Так    как,    магнитная    система    ТГ    представляет    собой нелинейную цепь, то влияние реакции якоря, в общем случае, является функцией двух переменных тока возбуждения и тока якоря, которую запишем в виде: F_A=f₂(I_Br,I_r),       (2.5)

Тогда аналогичную  функцию  в  воздушном  зазоре  можно определить из следующей функциональной зависимости:

B_б=f₁[I_ВГW_вг -f₂(I_ВГ,I_г)]       (2.6)

где W_BГ - число витков обмотки возбуждения ТГ.

Если вместо B_бввести в формулу (2.3) выражение (2.6), то получим:

 E_г=С_еГU_Г{f₁[I_ВГW_ВГ-f₂(I_ВГ,I_Г)]}         (2.7)

После   подстановки   выражения   (2.7)   в   (2.1),   уравнение математической модели нагружения ТГ будет иметь вид:

U_Г=C_enГ{f_l[l_BГW_BГ -f₂(l_BГI_Г)]}I_ГR_Г -2U_Щ,(2.8)

Функциональную зависимость (2.6) представляем следующим образом:

f₁[I_ВГW_ВГ-f₂(I_ВГ,I_U)]=f₁(I_ВГ,W_ВГ)-f₁[f₂(I_ВГ,I_Г)]

f₁(I_ВГW_ВГ)C_ЕГn_Г=E_гх

f₁[f₂(I_ВГ,I_Г) C_ЕГn_Г=∆E

Тогда уравнение модели (2.8) можно записать так:

U_Г=E_гх-∆E- I_ГR_Г,        (2.10)

где Е_ГХ - ЭДС ТГ при холостом ходе, В;

Е - величина, учитывающая реакцию якоря, В. При переходе к понятию полного падения напряжения в цепи якоря ∆U_Г =∆Е + I_ГR_Г +2U_щ, окончательное уравнение модели примет вид:

U_г= E_гх -∆U,    (2.11)

Для того чтобы эта модель была содержательной, объекту необходимо очень точно учитывать полное падение напряжения.

Рассмотрим на оси F отрезок OF, равный в масштабе н.с. F главного полюса и восстановим перпендикуляр до пересечения с кривой.

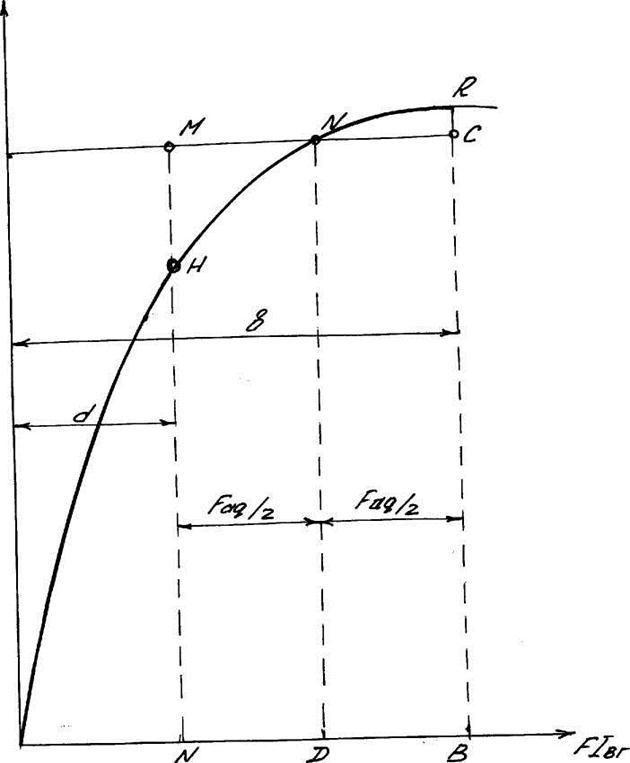
Точка и характеризует индукцию B_вв воздушном зазоре ТГ. При некотором токе якоря I_Г возникает поперечная н.c.

F_aq=atA,         (2.12)

где А = 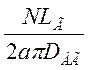 - линейная тяговая нагрузка;

D_АГ - диаметр якоря ТГ.

Они вызывают ослабление магнитного потока под одним краем магнитного потока над другим главного полюса ТГ. Если отложить на рис 2.1 вправо и влево от точки Р отрезок PN и РД, равные -, то кривая HKR покажет распределение индукции под полюсом. Площадь S_MiRD, ограниченная этой кривой, является энергией этого магнитного потока при действии по прямой реакции якоря, тогда как площадь S_mcp- при холостом ходе.

Очевидно, что уменьшение общего потока полюса будет определяться разностью этих площадей. Отсюда следует очевидное соотношение:

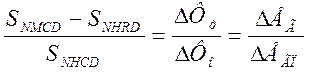
где Ф_о, E_ГП- магнитный поток главных полюсов и ЭДС якоря при холостом ходу, определяются из переходных кривых Ф₀=f(F)

Ф_р и Е_га - уменьшение потока и ЭДС при нагрузке.

При помощи наших расчетов реакция якоря определяется как функция двух переменных тока якоря 1_Г и тока возбуждения 1_Вг-

В данной работе предложен метод, который позволяет получить аналитическое уравнение площади криволинейной функции s_mRDиз переходной характеристики, апраксимированной сложным многочленом по методу наименьших квадратов.

Пусть     имеется     переходная     характеристика     E_ra=f(F), построенная   по   характеристике   холостого   хода   или   кривой намагничивания     O₀=f(F).     Как     известно,     суммарная     н.с, затрачиваемая на создание магнитного потока равна: F=F₆+F₃+F_c+F_n+F_я           (2.14)

где F_бF₃ - н.с. воздушного зазора и зубцового слоя якоря;

F_c,F_n,F_я - н.с. спинки якоря, полюсов сердечника и якоря.

Для получения переходной характеристики E_rn=f(F) исключим магнитные сопротивления сердечников, полюсов и якоря генератора, т.е. считаем, что апроксимируя эту зависимость сменным многочленом:

                        Е_ГП =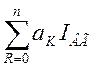 (2.15)

К = 1.2.3.....n

Реакцию   якоря   выразим   через   эквивалентный   ток   обмотки возбуждения генератора:

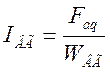                                   (2.16)

Тогда площадь криволинейной функции S_nhrd запишем в виде:

  S_nhrd=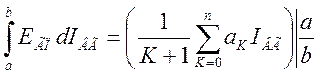         (2.17)

где a,b - пределы интегрирования, равные:

     a=I_ВГ-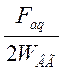     (2.18)

     b= I_ВГ-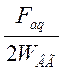     (2.19)

С другой стороны, предел а и b можно выразить через токи 1_ВГ и 1_Г, заменив значения н.с. F_aq формулой (2.12), подставив, получим:

                 а=1_Вг-К_г1г  (2.20)

                  в=1_вг+К_г1_г (2.21)

где к_г =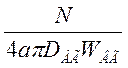коэффициент генератора.

Таким образом, величина реакции якоря представляется как функция двух переменных - тока возбуждения 1_ВГ и тока якоря 1_Г, которую можно определить аналитически из соотношения (2.13) подставив в него значения площади из (2.17):

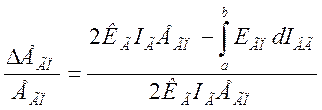              (2.22)

ИЛИ

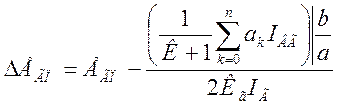            (2.23)

Полное сопротивление цепи якоря ТГ принятое для следующих расчетов, равно:

Rr⁼K_шт{R_дг+R_дп)=4,065* 10^-3 Ом    (2.24)

Где Кщт - поправочный коэффициент, полученный из анализа нагрузочных характеристик генераторов ГП311Б.

Из экспериментальных данных можно сделать вывод, что в реальном генераторе появляется не только поперечная, но и продольная реакция якоря, потому, что с ростом насыщения магнитной системы ее величина не изменяется.

Продольная реакция якоря зависит от угла поворота щеток относительно геометрической нейтрали, которой является случайной величиной. В связи с этим, предлагается определить полное падение напряжения в цепи якоря ТГ по экспериментальным данным, в которых участвуют все виды падений напряжения:

 ∆U= ∆E_Г+l_ГR_Г+2U_щ

Наилучшее приближение к экспериментальным данным, которые учитывают все виды падения напряжения, получается, по функции двух переменных следующего вида:

 ∆U=g_ГЕ_ГХI_Г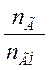 (2.24)

где Пг,Пгм — фактическая и максимальная скорость вращения ТГ;

g_Г=0,91 10^-8 - поправочный коэффициент. Для упрощения расчетов характеристики холостого хода ТГ опроксимированны степенным многочленом: Е_гх=6+14,31вг-0,1I_дг²+0,25 10^-3I_ВГ³   (2.25)

Тогда уравнение математической модели с учетом (2.24) и (2.25) будет иметь вид:

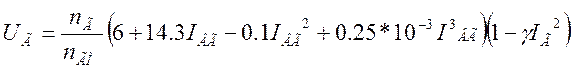(2.26)

Расчетные данные, полученные по формуле (2.24) приведены в табл. 2.1.

Таблица2.1

Расчетные значения		[ полного падения напряжения,			В
Ток	Ток возбуждения, А
якоря,А	20	40	60	80	100	120
1000	2,33	4,02	5,12	5,88	6,35	6,6
2000	9,34	15,90	20,50	23,50	25,40	26,4
3000	21,03	36,80	46,10	52,90	57,20	-
4000	37,40	63,70	81,90	94,00	-	-
5000	68,40	89,5	128,10	-	-	-
6000	84,10	113,2	-	-	-	-

Таблица 2.2

Полное падение напряжения в			цепи ТГ, В
Ток	Ток возбуждения, А
якоря,А	20	40	60	80	100	120
1000	4,4	5	81	8	7	6,5
2000	10	18,3	21	24	23,8	23,5
3000	15,8	32	43,1	42,4	40,8	-
4000	35,3	54	78,2	76	-	-
5000	60	98,7	114,3	-	-	-
6000	71	119,3	-	-	-	-

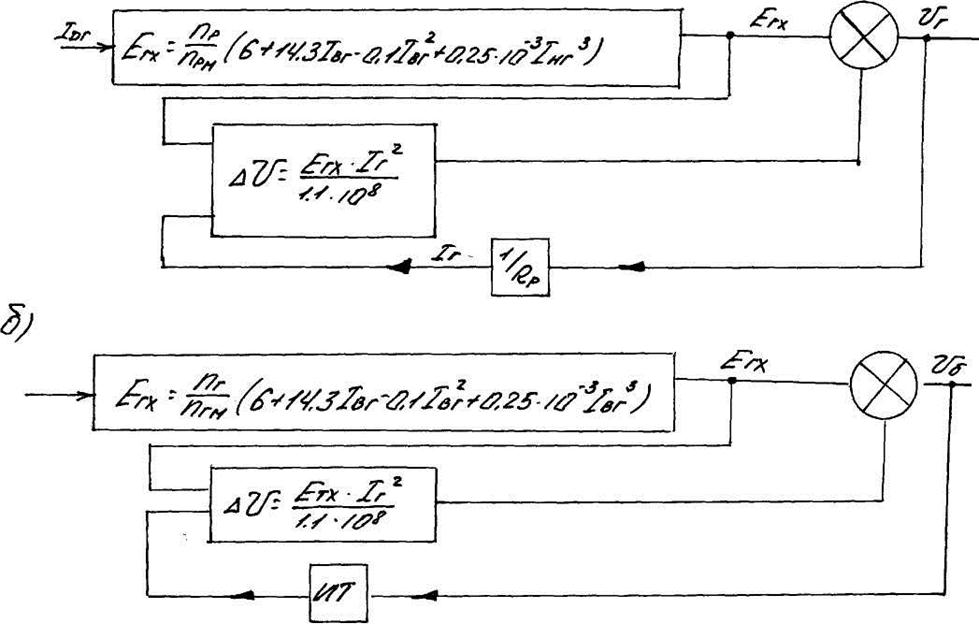
Как видно из таблиц 2.1 и 2.2 полученная зависимость очень точно воспроизводит падение напряжения и реакции якоря ТГ. Погрешность апроксимации нагрузочных характеристик в рабочем диапазоне тока и напряжения не превышает 1-4%.

вывод

Математическое регулирование работы ТГ путем создания математической модели ТГ позволяет регулировать параметры электрической передачи тепловоза и ее гиперболическую настройку без сложных реостатных испытаний. Что позволяет сэкономить энергоносители (дизельное топливо) и улучшить эксплуатацию тепловоза по всем тягово-энергетическим показателям.

Применение безреостатных испытаний ДГУ и ЭП тепловоза позволит сэкономить средства депо и дает большой экологический эффект в области локомотивостроения и эксплуатации тепловозов.