Несобственные интегралы. Вычисление несобственного интеграла от неограниченной функции

ПЛАН

Введение

1. Определение

2. Исследование функции, заданной интегралом.

3. Вычисление несобственного интеграла от неограниченной функции.

4. Несобственные интегралы I рода - интегралы с бесконечными пределами интегрирования

5. Несобственные интегралы II рода – интегралы от неограниченных функций

6. Решение типовых примеров

Литература

Введение

При определении определенного интеграла предполагалось, что:

1) отрезок интегрирования конечен;

2) функция непрерывна на отрезке интегрирования.

Если нарушено одно из этих условий, то определенный интеграл называется несобственным, причем если отрезок интегрирования неограничен, то интеграл называется несобственным интегралом первого рода, если же функция не ограничена на отрезке интегрирования, то несобственным интегралом -  второго рода.

1. Определение

С геометрической точки зрения, несобственные интегралы выражают площади неограниченных фигур.

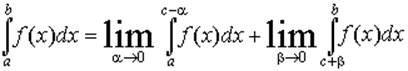
Интеграл как функция верхнего предела ~Несобственные интегралы по неограниченному промежутку ~ Несобственные интегралы от неограниченных функций ~ Исследование несобственных интегралов на сходимость

Интеграл как функция верхнего предела.

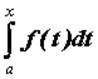Для функции , интегрируемой для всех , значение интеграла зависит от значения верхнего предела ; можно рассмотреть функцию переменной : каждому значению ставится в соответствие число, равное значению интеграла 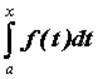. Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: ; функция определена в области интегрируемости подынтегральной функции . Если — первообразная для , то значение можно вычислить по формуле Ньютона—Лейбница: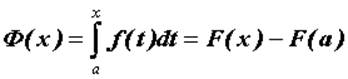 . Функцию 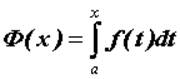можно исследовать, не вычисляя первообразной. Для интегрируемой при функции справедливы следующие утверждения: непрерывна на промежутке , причем ; если при , то   монотонно возрастает на промежутке ; если непрерывна при , то дифференцируема на промежутке , причем .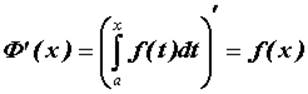

2. Исследование функции, заданной интегралом.

Несобственные интегралы по неограниченному промежутку.

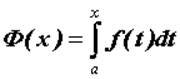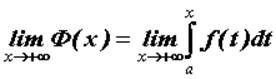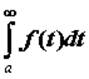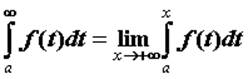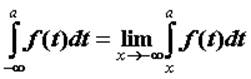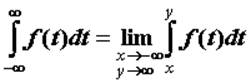Пусть функция интегрируема для всех и  . Если существует предел , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл для интегрируемой при функции и интеграл для функции , интегрируемой на . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.

ПРИМЕР 2.  Вычисление несобственного интеграла с бесконечным пределом.

Несобственные интегралы от неограниченных функций.

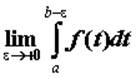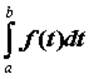Пусть функция интегрируема на любом отрезке, целиком содержащемся в промежутке , и бесконечно большая в точке . Если существует предел , то этот предел называют несобственным интегралом от неограниченной функции по и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле 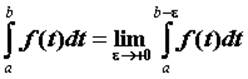. Аналогично определен интеграл 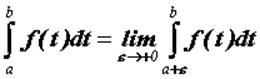от интегрируемой на любом конечном отрезке, содержащемся в , бесконечно большой в точке функции . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.

3. Вычисление несобственного интеграла от неограниченной функции.

Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен.

Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.

Рассмотрим две неотрицательные функции и , определенные при . Пусть для всех , начиная с некоторого числа . Тогда, если сходится интеграл от большей функции 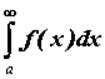, то сходится и интеграл от меньшей, то есть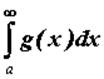. Если расходится интеграл от меньшей функции 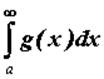,то расходится и интеграл от большей - .

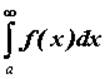Если 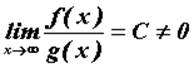 , то несобственные интегралы от этих функций или оба сходятся