









Проектом называют совокупность работ, направленных на достижение некоторой цели. Работы проекта, как правило, частично упорядочены. Выполнение работы не может быть начато до завершения всех предшествующих ей работ. Продолжительность выполнения каждой работы известна. Предполагается, что начатая работа продолжается без перерыва до ее завершения. Проект считается выполненным, если выполнены все его работы.
Сетевая модель – это графическое представление проекта. Она позволяет найти минимальные сроки завершения проекта и отдельных работ, а также определить множество критических работ, увеличение продолжительности выполнения любой из которых приводит к увеличению времени выполнения всего проекта.
Пример 3.1. (строительство дома). При строительстве дома необходимо выполнить такие работы, как создание подъездных дорог, подготовка котлована, возведение фундамента, подводка коммуникаций, монтаж здания, крыши, отделочные работы и т. п. Каждую работу проекта можно начать выполнять только после завершения всех предшествующих ей работ. Например, фундамент возводится только после подготовки котлована. В то же время некоторые работы, например подводка коммуникаций и отделочные работы, могут осуществляться параллельно.
Сетевая модель проекта представляет собой графическое описание плана работ, показывающее взаимосвязь между всеми работами, выполнение которых необходимо для завершения проекта. В терминах теории графов сетевая модель – это ориентированный граф без контуров и петель с неотрицательными весами вершин или дуг.
При анализе проектов используются два типа сетевых моделей, которые условно можно назвать: 1) «работы-вершины»; 2) «работы-дуги».
В сетевой модели первого типа вершины являются образами работ, а дуги служат для отображения отношения предшествования между работами.
В модели второго типа, наряду с работами-дугами, рассматриваются также новые понятия – события, которым соответствуют вершины сети.
Событие отражает результат – завершение одних работ и возможность начала других.
Направление дуги сети задает отношение предшествования работ проекта.
Указанные выше модели являются эквивалентными в том смысле, что для любого проекта можно построить как одну, так и другую модель.
В данном пособии, как и в [1, 3], рассматриваются сетевые модели типа «работы-дуги». В таких моделях для задания соотношения предшествования работ-дуг часто приходится вводить фиктивные дуги нулевой длины (продолжительность выполнения соответствующих фиктивных работ равна нулю). Нефиктивные дуги будем называть также фактическими.
Определение 3.1. Сети с одним и тем же множеством фактических дуг назовем эквивалентными, если они задают одно и то же отношение предшествования дуг-работ.
Вершину, не имеющую входящих в нее дуг, будем называть входом, а вершину, из которой не выходит ни одной дуги, – выходом сетевой модели. Без ограничения общности можно считать, что сетевая модель имеет один вход и один выход. Если исходная сеть не обладает этим свойством, то можно ввести фиктивный вход (выход) и связать с ним все входы (выходы) фиктивными дугами. Полученная сеть, очевидно, эквивалентна исходной сети.
Пример 3.2. Привести сетевую модель, изображенную на рис. 3.1 к эквивалентной сети с одним входом и одним выходом.
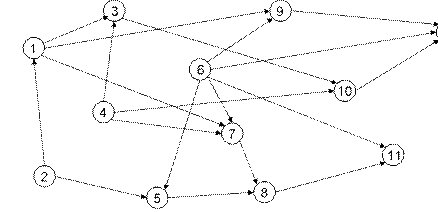
Рис. 3.1
Решение. Входами сети являются вершины 2, 4 и 6. Введем дополнительную вершину 13 и свяжем ее фиктивными дугами (13, 2), (13, 4) и (13, 6) со всеми входами.
Вершины 11 и 12 являются выходами сетевой модели. Добавим вершину 14 и соединим с ней фиктивными дугами (11, 14), и (12, 14) все выходы сетевой модели.
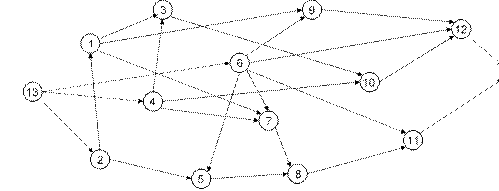
Рис. 3.2
На рис. 3.2 представлена новая сеть с одним источником 13 и одним стоком 14. Фиктивные дуги изображены пунктирными линиями.
В ряде случаев исходную сеть можно упростить, исключив часть вершин и фиктивных дуг. Введем следующие обозначения:
S = (X U, ) – сеть с множеством вершин X и множеством дуг U; i(j) – начальная вершина дуги j; k(j) – конечная вершина дуги j;
![]()
U – множество фактических дуг сети;
![]() Ui– множество дуг из U , принадлежащих объединению всех путей из входа
сети в вершину i;
Ui– множество дуг из U , принадлежащих объединению всех путей из входа
сети в вершину i;
Ui– множество дуг из U , принадлежащих объединению всех путей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.