Если каждому x из множества E поставлено в
соответствие некоторое число f(x), то мы будем говорить, что на множестве E задана
функция f(x). При этом мы допускаем и бесконечные
значения функции, лишь бы они имели определенный знак, т.е. вводим
«несобственные» числа -![]() и +
и +![]() . Эти
числа связаны между собой и с любым конечным числом a
неравенствами
. Эти
числа связаны между собой и с любым конечным числом a
неравенствами
-![]() <a<+
<a<+![]() , и мы устанавливаем для них следующие законы действий:
, и мы устанавливаем для них следующие законы действий:
+![]() ±a=+
±a=+![]() , +
, +![]() +(+
+(+![]() )=+
)=+![]() , +
, +![]() -(-
-(-![]() )=+
)=+![]() ,
,
-![]() ±a=-
±a=-![]() , -
, -![]() +(-
+(-![]() )=-
)=-![]() , -
, -![]() -(+
-(+![]() )=-
)=-![]() ,
,
½+![]() ½=½-
½=½-![]() ½=+
½=+![]() , +
, +![]() ×a=a×(+
×a=a×(+![]() )=+
)=+![]() ,
,
-![]() ×a=a×(-
×a=a×(-![]() )=-
)=-![]() , если a>0,
, если a>0,
+![]() ×a=a×(+
×a=a×(+![]() )=-
)=-![]() ,
,
-![]() ×a=a×(-
×a=a×(-![]() )=+
)=+![]() , если a<0
, если a<0
0×(±![]() )=(±
)=(±![]() )×0=0,
)×0=0,
(+![]() )×(+
)×(+![]() )=(-
)=(-![]() )×(-
)×(-![]() )=+
)=+![]() ,
,
(+![]() )×(-
)×(-![]() )=(-
)=(-![]() )×(+
)×(+![]() )=-
)=-![]() ,
,
![]() =0.
=0.
Здесь a обозначает вещественное конечное число. Символы
+¥-(+¥), -¥-(-¥), +¥+(-¥), -¥+(+¥).
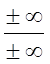 ,
, ![]()
мы считаем лишенными смысла.
Имея дело с функцией f (x), заданной на множестве E, мы будем символом
E(f>a)
обозначать множество тех x из множества Е, для которых выполнено неравенство f(x)>а.
Аналогичным образом вводятся символы
Е(f³а), Е(f=а), Е(f£а), Е(а<f£b)
и т.п. Если множество, на котором задана функция f(x), обозначено какой-либо другой буквой, например А или В, то мы соответственно будем писать
А(f>а), В(f>а)
и т.п.
Определение 1. Функция f(x), заданная на множество Е, называется измеримой, если измеримо это множество Е и если при любом конечном а измеримо множество
Е(f>а).
В связи с тем, что здесь речь идет о множествах, измеримых в смысле Лебега, часто (желая подчеркнуть именно это обстоятельство) говорят об измеримой (L) функции. Если же Е и все множества Е(f>а) измеримы (В), то и f(x) называется измеримой (В) функцией.
Теорема 1. Всякая функция, заданная на множестве меры нуль, измерима.
Это утверждение очевидно.
Теорема 2.Пусть f(x) есть измеримая функция, заданная на множестве Е. Если А есть измеримое подмножество Е, то f(x), рассматриваемая только для xÎА, измерима.
Действительно, А(f>а) =А×Е (f>а).
Теорема 3.Пусть f(x) задана на измеримом множестве Е, представимом в форме суммы конечного числа или счетного множества измеримых множеств Еk :
E=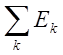 ×
×
Если f(x) измерима на каждом из множеств ER., то она измерима и на Е.
В самом деле, E(f>a)= 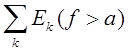 .
.
Определение 2. Две функции f(x) и g(x), заданные на одном и том же множестве Е, называются эквивалентными, если
mE (f¹g)=0
Обозначать эквивалентность функций f(x) и g(x) принято так:
f (x) ~g(x).
Определение 3. Пусть некоторое обстоятельство S имеет место для всех точек какого-нибудь множества Е, кроме точек, входящих в подмножество Е0 множества Е. Если mЕ0 = 0, то говорят, что S имеет место почти везде на множестве Е, или почти для всех точек Е.
В частности, множество исключительных точек Е0 может быть и пустым.
Теперь можно сказать, что две функции, заданные на множестве Е, эквиваленты, если они ровны почти везде на Е.
Теорема 4. Если f(х) есть измеримая функция, заданная на множестве Е, а g(x) ~ f(x), то g(x) также измерима.
Д о к а з а т е л ь с т в о. Пусть А = Е (f ¹ g), B = E – A. Тогда mA = 0, так что В измеримо. Значит функция f(x) измерима на множестве В. Но на множестве В функции f(x) и g(x) неотличимы, так что g(x) измерима на В. Поскольку g(x) измерима и на А (ибо mA = 0), она измерима на Е = А + В.
Теорема 5. Если для всех точек измеримого множества Е будет f(x) = c, то функция f(x) измерима.
Действительно,
E
(f > a) = ![]()
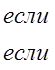
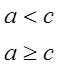
Заметим, что в этой теореме с может быть и бесконечным.
Функция f(x), заданная на сегменте [а, b], называется ступенчатой, если [а,b] разложить точками.
с0 = а< с1<с2<…<сn = b
на конечное число частей, в н у т р и которых (т.е. в интервалах (сk, ck + 1) при k = 0, 1, …., n –1) функция f(x) постоянна. Легко понять, что из теоремы 5 вытекает
Следствие. Ступенчатая функция измерима.
Теорема 6. Если f(x) есть измеримая функция, заданная на множестве Е, то при любом а измеримы множества
E (f ³ a), E (f = a), E (f £ a), E (f < a),
E (f ³ a) = 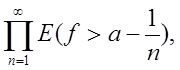
E (f = a) = E(f ³ a) – E(f > a), E(f £ a) = E – E(f > a),
E (f < a) = E – E (f ³ a).
Замечание. Легко показать, что если хоть одно из множеств
E (f ³ a), E (f £ a), E (f < a)
оказывается измеримым при всяком а, то функция f(x) измерима на множестве Е (которое также предполагается измеримым).
Действительно, тождество 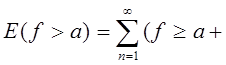
![]() ) показывает, например, что f(x)
измерима, если измеримы все множества Е (f³а). Сходным образом
устанавливаются и остальные утверждения. Таким образом, в определении измеримой
функции можно заменить множество Е (f>a)
любым из множеств (1).
) показывает, например, что f(x)
измерима, если измеримы все множества Е (f³а). Сходным образом
устанавливаются и остальные утверждения. Таким образом, в определении измеримой
функции можно заменить множество Е (f>a)
любым из множеств (1).
Теорема 7. Если функция f(x), заданная на множестве Е,
измерима, а kконечное число, то
измеримы и функции 1) f(x) + k, 2) kf(x), 3) çf (x)ç, 4) f2 (x), и если f(x) ¹0, то измерима и функция
5) ![]() .
.
Д о к а з а т е л ь с т в о. 1) Измеримость функции f(x) + k вытекает из соотношения Е (f+ k >a) = E (f>a- k).
2) Измеримость функции kf(x) при k =0 следует из теоремы 5. Для прочих k измеримость следует из очевидных соотношений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.