Производная, и ее применение

                                     Реферат.

                     на тему “Производная,  и  ее применение ”.

                                                              Успенского Сергея   

 Определение производной

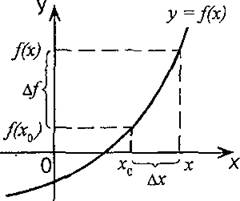
  Пусть х - произвольная точка, лежащая в некоторой окрестности точки Х0 (окрестность точки Х0 - это интервал (а; б), x0Î(а; 6)).

Разность х-Х° называется приращением аргумента:

∆x = х-x0. Отсюда x = x0 + ∆x.

  Разность f(x)-f(x0) называется приращением функции:

∆f = f(x) - f(x0) или 

∆ f = f(x0+∆x) – f(x0).

Отсюда f (x0+∆x) = f (x0) + ∆ f.

   Геометрический смысл приращений ∆х и ∆ f  показан на рисунке .    Производной функции y = f(x) в точке x0 называется предел отношения   приращения функции ∆f к приращению аргумента ∆x, стремящегося к "нулю."

Обозначается f ' (x0). Читается: "эф штрих в точке x0. Итак,

 f ' (x0) = lim (∆ f / ∆x)

               ∆x→ 0

  Если функция у = f (х) имеет производную в точке x0 , то                    говорят, что она дифференцируема в точке x0.

  Нахождение производной данной функции называется дифференцированием.

 Правила дифференцирования.

1. Если функции u и v дифференцируемы в точке x0, то их сумма также дифференцируема в точке x0, причем производная суммы равна сумме производных, т.е.

(u + n)'=u' + n'.

2. Если функции u и v дифференцируемы в точке x0, то их произведение также дифференцируемо в точке x0 причем

(u - n)' = u'n + un'.

3. Если функции u и n дифференцируемы в точке х0 и  

n'(x0) ≠ 0, то их частное также дифференцируемо в точке x0, причем  (u/n)' = (u'n - un') / n²

4. Если функция и дифференцируема в точке x0 и с = const. то их произведение также дифференцируемо в точке x0 причем  (сu)' = си'.

5. Если f (g(х)) - сложная функция, то ее производная равна произведению производных внешней и внутренней функций, т.е.

[f(g(x))]'= f '(g) ◦ g'(x).

 Физический смысл производной.

Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t0; t0+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве   при ∆t → 0.

lim Vср (t) = n(t0) - мгновенная скорость в момент времени t0,  ∆t → 0.

а lim  = ∆x/∆t = x'(t0) (по определению производной).

Итак, n(t) =x'(t).

Физический смысл производной заключается в следующем: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0

Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.

u(t) = x'(t) - скорость,

a(f) = n'(t) - ускорение, или

a(t) = x"(t).

Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:

φ = φ(t) - изменение угла от времени,

ω = φ'(t) - угловая скорость,

ε  = φ'(t) - угловое ускорение, или ε = φ"(t).

Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:

m = m(х) - масса,

x Î [0; l], l - длина стержня, р = m'(х) - линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука

F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω² =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω²x(t) = 0, где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m).

Уравнение вида у" + ω²y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция у = Asin(ωt + φ0) или у = Acos(ωt + φ0), где

А - амплитуда колебаний, ω - циклическая частота,

φ 0 - начальная фаза.

Элементы исследования функции с помощью пределов и производной.

С помощью производной функции устанавливают промежутки монотонности, точки экстремума, наибольшее и наименьшее значения функции на отрезке.

При этом используются следующие теоремы:

1. Если f ' (х) > 0 в каждой точке интервала I, то функция возрастает на I. Если f ' (х) < 0 в каждой точке интервала I, то функция убывает на I.

2. Теорема Ферма (необходимое условие экстремума): если x0- точка экстремума и в этой точке существует производная, то она равна нулю.

Определение. Внутренняя точка области определения, в которой производная равна нулю или ее не существует, называется критической.

3. Достаточное условие экстремума: если функция f (x) непрерывна в точке x0, а f '(х) > 0 на интервале (а; x0)

f '(х) < 0 на интервале (x0; b), то точка x° является точкой максимума