В основе метода лежит идея рассмотрения исходной задачи как представителя семейства сходных с ней задач. Динамическое программирование (ДП) связано с многошаговым (многоэтапным) процессом принятия решений. При этом под многошаговым процессом принятия решений понимается деятельность, при которой принимаются последовательные решения, направленные на достижение одной цели. Методу ДП посвящено множество публикаций, в частности работы [1, 2, 5], в которых достаточно подробно рассмотрена техника решения задач методом динамического программирования.
В данном разделе мы будем изучать метод постепенно по принципу «от простого к сложному». Начнем с распределительной задачи.
Сформулируем распределительную задачу на примере планирования деятельности предприятия на n лет. Пусть предприятие имеет ресурс в размере Y единиц, который оно может вложить в производство в течение n лет. Функции ft(x) отражают эффективность использования x единиц ресурса в год t. Требуется определить план расхода имеющегося ресурса по годам, чтобы максимизировать суммарную эффективность.
Обозначим через хt искомую величину ресурса, вкладываемого в развитие производства в год t = 1, …, n. Тогда математическая модель может быть записана в виде
n
|
ft(xt) →max ;
|
(2.1) |
|
n ∑ xt ≤ Y; t=1 |
(2.2) |
|
xt ≥ 0, t = 1, ..., n. |
(2.3) |
Решение задачи (2.1)−(2.3) будем строить шаг за шагом, оптимизируя на текущем шаге размер инвестиций в год t. Будем предполагать функции ft(x) неубывающими, что позволяет перейти от исходной задачи к равносильной задаче (2.1), (2.2′), (2.3), в которой неравенство (2.2) заменено равенством
n
∑ xt = Y.(2.2′)
t=1
Для задачи (2.1), (2.2′), (2.3) используем обозначение <n, Y>. Кроме того, обозначим:
− S* – оптимальное значение целевой функции (2.1);
, …, x*n )
– оптимальное решение рассматриваемой задачи, т. е.
n
S* 
));
k=1 k
оптимальное вложение ресурса за k
первых лет,
i=1
k = 1, …, n.
Далее воспользуемся терминологией и обозначениями из [2]. Наряду с
исходной задачей <n, Y> рассмотрим семейство задач
π = {<k, y>: k = 1, …, n; 0 ≤ y ≤ Y}. Пусть Sk(y) – оптимальное значение целевой функции задачи <k, y>, тогда S*= Sn(Y).
Теорема 2.1. Для задачи (2.1), (2.2′), (2.3) справедливы следующие рекуррентные соотношения ДП:
S1(y) = f1(y), 0 ≤ y ≤ Y;(2.4)
Sk
,
k = 2, …, n; 0 ≤
y ≤ Y.(2.5)
Значение переменной x, при котором достигается максимум в (2.5), обозначим через xk(y) и назовем условно-оптимальным решением.
*
Следствие 2.1. Условно-оптимальное решение xk(y k ) является оптимальным значением k-й компоненты вектора x* исходной задачи <n, Y>,
* *
т. е. x k = xk(y k ), k = 1, …, n.
Алгоритм ДП состоит из прямого хода (процесса последовательного вычисления величин Sk(y), k = 1, …, n; 0 ≤ y ≤ Y) и обратного хода (восстановления оптимального решения). На последнем шаге прямого хода полу-
* чаем оптимальное значение последней переменной x n = xn(Y). Пусть уже
* * * * найдены оптимальные значения x n , …, x k+1 . Тогда x k = xk(y k ),где
* * *
y k = y k+1− x k+1.
Схема (2.4), (2.5), как правило, требует численного расчета, но иногда удается получить выражение функций Sk(y) в аналитическом виде.
Пример 2.1. Рассмотрим метод ДП для задачи (2.1)−(2.3) с функциями
xi2 fi(xi)= 
, где ci > 0 и i = 1, …, n. ci
y2
Прямой
ход. На первом шаге получаем S1(y) = 
и
условно-
c1
оптимальное решение x1(y) = y. Далее
2 2 x (y − x)
S2(y)
= min {f2(x) + S1(y −
x)}= min { + }.
0≤ ≤x y 0≤ ≤x y c2 c1
Выражение в фигурных скобках представляет
выпуклую функцию, минимум которой можно найти, приравняв нулю ее производную. Получим
x y x− c
y2 y2
− = 0, откуда x2(y)
= , а S2(y) = 
.
c2 c1 c1 +c2 c1 +c2
С помощью математической индукции нетрудно доказать, что
y2 c yk
Sk(y)
= 
k ,
xk(y) = k , 0 ≤ y ≤ Y.
∑ci ∑ci
i=1 i=1
Таким образом,
* Y
2c Yn
|
∑ci i=1 |
∑ci i=1 |
S
= Sn(Y) = n , x =
n .
*
Обратный ход. Зная оптимальное значение последней переменной xn , находим
n n−1
Y c c Y∑ i − n Y∑ci
y*n−1=Y−
x*n =Y−
c Ynn = i=1 n = ni=1 .
∑ci ∑ci ∑ci i=1 i=1 i=1
Следовательно,
c Yn−1
x. n
∑ci
i=1
Воспользовавшись математической индукцией, получим
x *k
= c Ynk ,
k = 1, …, n.
∑ci
i=1
В общем случае для реализации алгоритма ДП нужна дискретность значений xk. Пусть переменные xk целые. Тогда величины y также целые. Следовательно, параметру y достаточно принимать значения из конечного множества {0, 1, …, Y}. Трудоемкость алгоритма в этом случае равна O(nY2), а требуемая память – O(nY).
Пример 2.2. На железнодорожную станцию прибыло 8 контейнеров, которые необходимо развезти по 5 складам. Емкость i-го склада – vi контейнеров, затраты на транспортировку одного контейнера на этот склад – gi, а стоимость хранения x контейнеров – ci(x). Требуется развезти все прибывшие контейнеры по складам, чтобы суммарные затраты на транспортировку и хранение были минимальны.
Исходные данные задачи приведены в табл. 2.1 и 2.2.
|
Склады |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
gi |
0,5 |
1 |
1,2 |
1,5 |
2 |
|
vi |
2 |
3 |
3 |
5 |
5 |
|
x |
c1(x) |
c2(x) |
c3(x) |
c4(x) |
c5(x) |
|
1 |
2 |
1,5 |
1 |
0,5 |
0,3 |
|
2 |
4 |
2 |
2 |
1 |
0,5 |
|
3 |
− |
3 |
3 |
1,5 |
1 |
|
4 |
− |
− |
− |
2 |
1,5 |
|
5 |
− |
− |
− |
2,5 |
2 |
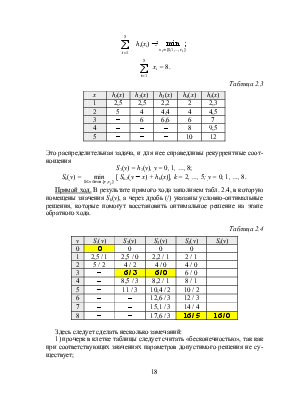
Решение. Для записи математической постановки задачи введем функции hi(x) = gix + ci(x), i = 1, …, 5, которые задаются табл. 2.3. Тогда математическая модель имеет следующий вид:
) →
min ;
xi∈{0,1,...,vi }
i=1
5
∑ xi = 8.
i=1
|
x |
h1(x) |
h2(x) |
h3(x) |
h4(x) |
h5(x) |
|
1 |
2,5 |
2,5 |
2,2 |
2 |
2,3 |
|
2 |
5 |
4 |
4,4 |
4 |
4,5 |
|
3 |
− |
6 |
6,6 |
6 |
7 |
|
4 |
− |
− |
− |
8 |
9,5 |
|
5 |
− |
− |
− |
10 |
12 |
Это распределительная задача, и для нее справедливы рекуррентные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
{x } t=1 t