Организация работы ПТОЛ в депо Москва – Сортировочная

2.Организация работы ПТОЛ в депо Москва – Сортировочная.

2.1Учебно-исследовательский раздел.

           Анализ поступления локомотивов в ПТОЛ в Москва - Сортировочная.

   Для исследования поступления локомотивов ПТОЛ были собраны материалы по заходу локомотивов. После сбора и обработки информации построим гистограмму.

  По этой гистограмме проведём исследования на определение вида закона распределения и расчёт оценок его параметров.

   При анализе и расчёте характеристик надёжности технических средств (локомотивов) приходится оперировать случайными величинами.  Это обусловлено тем, что отказ любой детали вызывает влияние целого ряда факторов, большинство из которых имеет случайную природу.

       Пусть в результате испытаний или наблюдений имеется информация об отказах или сохранений работоспособности объектом. Исходными  данными  для определения вида распределения обычно является эмпирическая плотность распределения, т.е. наблюдаемые значения случайной величины, сгруппированные по частоте проявления. Выбор вида или типа распределения должен основываться либо на прошлом опыте , либо на знании конкретного физического механизма появления отказа.

        В теории надёжности используют несколько способов определения вида закона распределения и расчёт оценок его параметров на основе данных об отказах.

       В том случае, если несколько теоретических распределений не дают существенного расхождения с эмпирическим, принимают тот закон распределения, который даёт наилучшую вероятность согласия.

         Чаще всего в качестве критерия согласия используют критерий X²( К. Пирсона). Который является наиболее приемлемым при достаточно большом числе наблюдений. Критерий X ²обычно применяют в тех случаях, когда теоретические значения параметров функции распределения неизвестны.

X²=(mj-mj’)²/m’j*k+I;   (2.1)

Где j=1,2,3,………., k – интервалы группирования случайной величины X  в выборочной совокупности объемом N значений;

mj=эмпирическая частота попаданий случайной величины в j-ый интервал.

m’j=NPj- теоретическая частота попадания случайной величины в j-ый

интервал.

Pj- теоретическая накопленная вероятность попадания случайной величины в j- интервал.

При расчётё критерия X^2 используется эмпирические выборочные данные mj и накопленный теоретические частоты m’j, найденные

j(X)=l*e- l*x;   (2.2)

l-параметр закона распределения.

Определяем среднее значение выборки

X=mjxj / mj;          (2.3)

Вычисляем параметр l

l=1 / X;           (2.4)

определяем значение lxj и заносим в таблицу. После чего определяем среднеквадратичное отклонение Sx

Sx= mj * (xj)² / mj - (x)²;         (2.5)

Коэффициент вариации

Vx=Sx \ x;           (2.6)

Теоретические значения частностей m’j по формуле.

m’j=mj * j (xj);           (2.7)

где h- величина интервала разбиения пробега.

    Полученные значения mj заносим в таблицу и вычислим  критерий X² . Экспоненциальный закон и для него число степеней свободы n = k-c-1;

В этом выражении K –число интервалов разбиения пробега.

 С-число параметров закона распределения.

n=10-1-1=8;      (2.8)

Выравнивание статистических данных в  марте 2006 г. экспоненциальным
		законом распределения
Интервалы	xi, мин	mi, шт	lxi	exp(-lxi)	j(xi)	mi',шт	(mi-mi')^2/mi'
1	30	20	0,4466	0,6398	0,00952	13,1	3,576
2	60	10	0,8932	0,4093	0,00609	8,4	0,301
3	90	8	1,3398	0,2619	0,00390	5,4	1,276
4	120	3	1,7864	0,1676	0,00249	3,4	0,057
5	150	3	2,233	0,1072	0,00160	2,2	0,289
6	180	2	2,6796	0,0686	0,00102	1,4	0,248
7
8
9
10
11
		46					5,746

Таб. 2.1

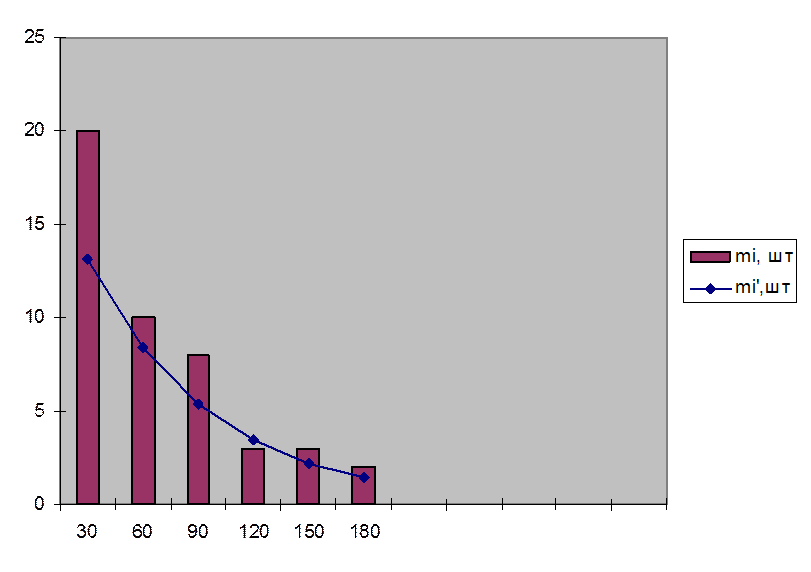
Рис. 2.1     Статистическое распределение интервалов времени между

заходами локомотивов в ПТОЛ в  марте 2006 г

для n=8 и доверительной вероятности 0,05по табл. П2,2 находим  X² =15,507

 В нашем случае X²= 5.746, что меньше X²=15.507   согласно критерию Пирсона

гипотеза о предположении , что случайная величина-интервал времени между поступлением локомотивов в ПТОЛ описывается экспоненциальным законом распределения, можно использовать расчётные формулы для этого распределения при расчётах параметров функционирования ПТОЛ как системы массового обслуживания. В наиболее часто решаемых задачах массового обслуживания отыскивается количество обслуживаемых каналов. При увеличении количества обслуживающих каналов затраты от простоязаявки в очереди снижаются , а затраты на ихсоздание и эксплуатацию увеличиваются. В системах массового обслуживания запрос обслуживания объекта на выполнение  какой- либо работы называется заявкой или требованием. Обслуживающий аппарат ( машина) , способный в любой момент времени удовлетворять только одну заявку, называется каналом обслуживания. Система  с очередями обычно задаются следующими исходными данными.

Вероятность свободности аппарата Р₀.

                            

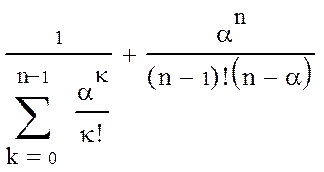
 при a/n<1.   (2.9)

  a/n<1- условие того, что очередь не будет неограниченно возрастать

P0=1/1+1+0.625²/2+0.625³/(2-1)*(2-0.625)=0.524.   

Вероятность того , что все обслуживающие аппараты заняты.

П=aⁿ/(n-1)!(n-a)*p0 при a/n<1.        (2.10)

 П=0,625³/(2-1)*(2-0.625)*0.524=0.149.         

              Математическое ожидания продолжительности простоя локомотива ;

Tож=П/m*(n-a) при a/n<1.             (2.11)

m= интенсивность обслуживания( число обслуживаний в единицу времени.)

n= число каналов.

a= плотность потока заявок( число поступающих заявок в единицу времени.)

Tож=0,149/1(2-0,625)=0,108час. 

Полученное теоретическим путём  математическое ожидание простоя локомотивов перед ПТОЛ.  Тоже 0,108 часа  может быть использована для определения технически обоснованной нормы времени нахождения локомотива в основном депо Москва – Сортировочная при планировании эксплуатационного парка локомотивов.