







Тестирование макросов
1. Графический метод решения задач линейного программирования
Применяется к задачам с двумя переменными. Состоит в построении многоугольника допустимых решений и визуального определения, если таковой существует, точек входа и выхода из него прямых уровня целевой функции.
Макрос на отдельном листе-диаграмме возвращает:
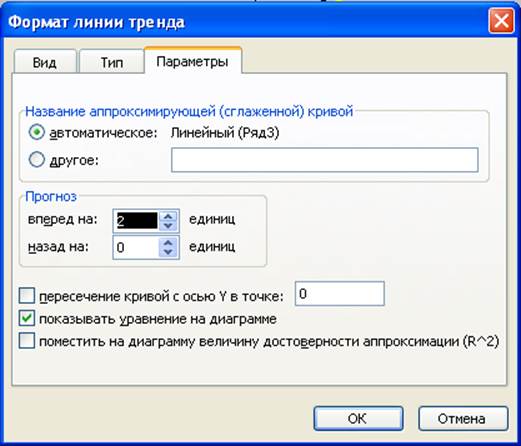
Граничные прямые в макросе строятся как линии тренда по координатам точек пересечения их с осями координат, то есть изображаются отрезками, продлеваемыми при необходимости через их контекстные меню [Формат линии тренда]/[Параметры], где задаются значения параметра “Прогноз”. По граничным прямым нетрудно определить существует или нет многоугольник допустимых решений. В первом случае, перенесением прямой уровня целевой функции, остается визуально определить точки, в которых целевая функция принимает оптимальные значения, и вычислить эти значения.
Тестирование на задаче:
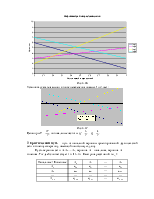
![]() ,
,
![]()
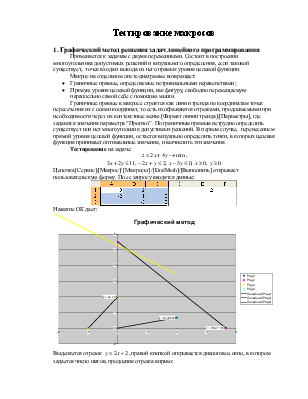
Цепочка [Сервис]/[Макрос]/ [Макросы] /[DrafMeth]/[Выполнить] открывает пользовательскую форму. По ее запросу вводятся данные:

Нажатие ОК дает:
Выделяется отрезок ![]() , правой кнопкой
открывается диалоговое окно, в котором задается число шагов, продления отрезка
вправо:
, правой кнопкой
открывается диалоговое окно, в котором задается число шагов, продления отрезка
вправо:
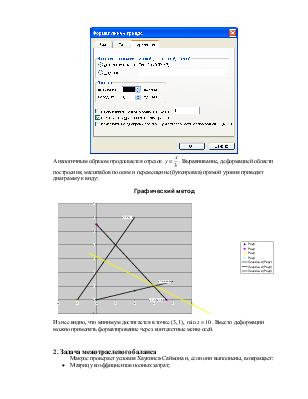
Аналогичным образом продлевается отрезок 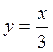 . Выравнивание,
деформацией области построения, масштабов по осям и перемещение (буксировка)
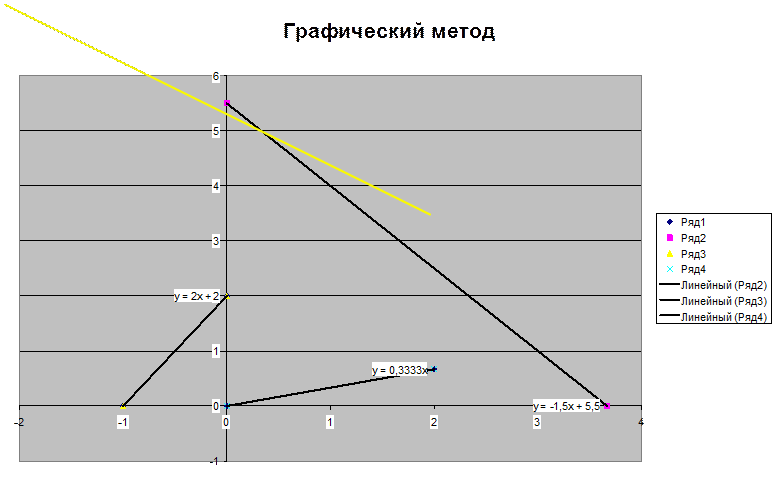
прямой уровня приводят диаграмму к виду:
. Выравнивание,
деформацией области построения, масштабов по осям и перемещение (буксировка)
прямой уровня приводят диаграмму к виду:
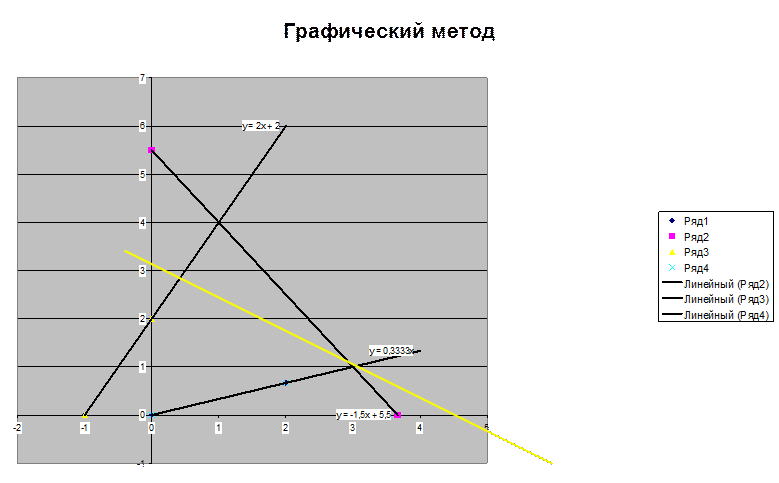
Из нее видно, что минимум достигается в точке
(3, 1), ![]() . Вместо деформации
можно применять форматирование через контекстные меню осей.
. Вместо деформации
можно применять форматирование через контекстные меню осей.
2. Задача межотраслевого баланса
Макроспроверяет условия Хаукинса-Саймона и, если они выполнены, возвращает:
Тестирование
Данные:
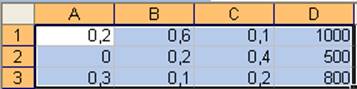
Результаты:
3. Транспортная задача
Стандартная
Найти план перевозок, минимизирующий транспортные расходы, по данным транспортной таблицы:
|
Запасы \ Потребности |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
………… |
……. |
…….. |
………. |
…….. |
|
|
|
|
… |
|
Задача может быть
как закрытой 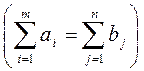 , так и
открытой
, так и
открытой 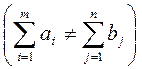 . В первом случае
ее математическая модель:
. В первом случае
ее математическая модель:
![]() , (1)
, (1)
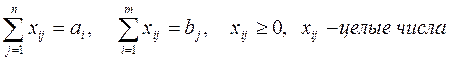 (2)
(2)
Во втором случае, если 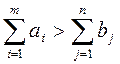 , ограничения (2)
заменяются ограничениями
, ограничения (2)
заменяются ограничениями
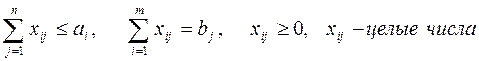 , (3)
, (3)
а если 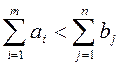 , то ограничениями
, то ограничениями
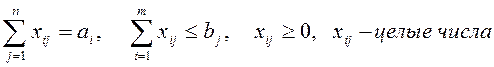 (4)
(4)
СредстваExcel открывают богатейшие возможности по решению транспортных задач с ограничениями, некоторые из которых приведены ниже и реализованы в проекте.
Ограничения на пропускные способности
Стандартная
транспортная модель, в которой для некоторых значений ![]() заданы
дополнительные ограничения
заданы
дополнительные ограничения
![]() . (5)
. (5)
Последние можно рассматривать как ограничения на грузоподъемность транспорта, доставляющего груз от i-го поставщика j-му потребителю. Такие модели, вычисления в которых достаточно трудоемки, не всегда имеют решения. Достаточным условием разрешимости является существование хотя бы одного допустимого решения.
Дополнительно заданный объем груза
Математическая модель:
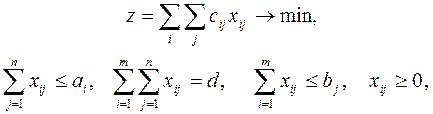 (6)
(6)
где натуральное число ![]() , удовлетворяет
условию
, удовлетворяет
условию
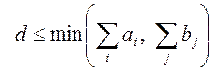
Допустим, надо
доставить однородный груз объемом ![]() через
таможни
через
таможни ![]() , с пропускными
способностями
, с пропускными
способностями ![]() , в
пункты
, в
пункты ![]() , с потребностями в
нем
, с потребностями в
нем ![]() , соответственно.
Матрица
, соответственно.
Матрица ![]() предполагается
известной. В этом случае решение модели (6) дает план перевозок
предполагается
известной. В этом случае решение модели (6) дает план перевозок ![]() , минимизирующий
транспортные расходы, и, соответственно, план размещения груза на таможнях:
, минимизирующий
транспортные расходы, и, соответственно, план размещения груза на таможнях: 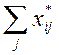 .
.
Если 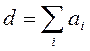 или
или 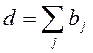 , то модель (6)
принимает вид (1, 3) или (1, 4), соответственно.
, то модель (6)
принимает вид (1, 3) или (1, 4), соответственно.
Приоритеты
Если 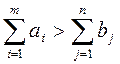 , то к соотношениям
(3) по некоторым значениям индекса
, то к соотношениям
(3) по некоторым значениям индекса ![]() ,
пробегаемым переменной
,
пробегаемым переменной ![]() ,
добавляются ограничения
,
добавляются ограничения
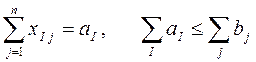 (7)
(7)
а если 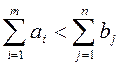 , то к соотношениям
(4) по некоторым значениям индекса
, то к соотношениям
(4) по некоторым значениям индекса ![]() ,
пробегаемым переменной
,
пробегаемым переменной ![]() ,
добавляются ограничения
,
добавляются ограничения
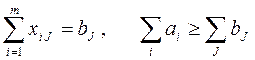 (8)
(8)
Ограничения (7, 8) появляются, например, тогда, когда транспортные сообщения с каким-либо поставщиком или потребителем ограничены по времени. То, что в определенный срок не вывезено – пропадает, то, что не завезено – позже восполнить нельзя, а значит, такие пункты должны быть обязательно закрыты.
Паритеты
Если 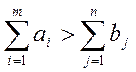 , то в (1, 3) для
некоторых значений
, то в (1, 3) для
некоторых значений ![]() добавляется
ограничение
добавляется
ограничение
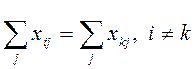 , (9)
, (9)
то есть из пунктов ![]() и
и ![]() вывозятся равные
объемы груза, а если
вывозятся равные
объемы груза, а если 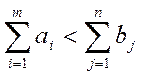 , то в
(1, 4) для некоторых значений
, то в
(1, 4) для некоторых значений ![]() добавляются
ограничения
добавляются
ограничения
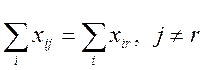 , (10)
, (10)
то есть в пункты ![]() и
и ![]() завозятся равные
объемы груза.
завозятся равные
объемы груза.
Ограничения (9, 10) появляются, например, тогда, когда груз – единицы вооружений и есть противоборствующие стороны.
Тестирование
1.Запуск макроса DemoTrans открывает окно:
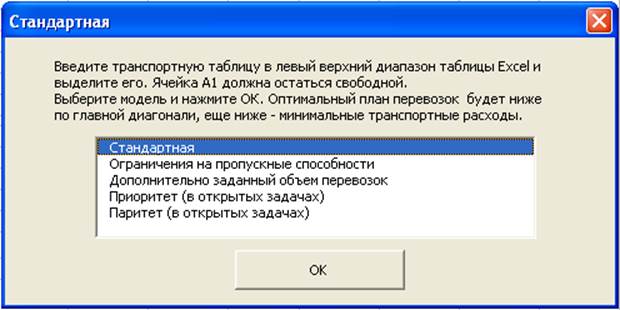
Вводится и выделяется транспортная таблица:
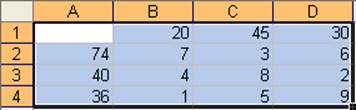
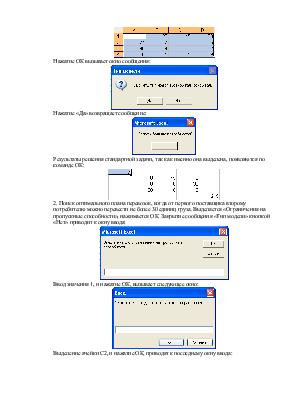
Нажатие ОК вызывает окно сообщения:
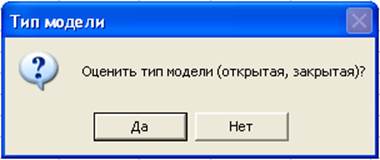
Нажатие «Да» возвращает сообщение:
Результаты решения стандартной задачи, так как именно она выделена, появляются по команде ОК:
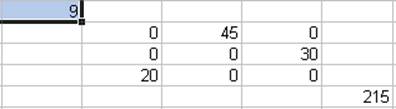
2. Поиск оптимального плана перевозок, когда от первого поставщика второму потребителю можно перевести не более 30 единиц груза. Выделяется «Ограничения на пропускные способности», нажимается ОК. Закрытие сообщения «Тип модели» кнопкой «Нет» приводит к окну ввода:
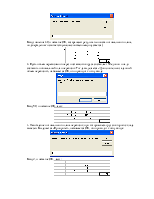
Ввод значения 1, и нажатие ОК, вызывает следующее окно:
Выделение ячейки С2, и нажатие ОК, приводят к последнему окну ввода:
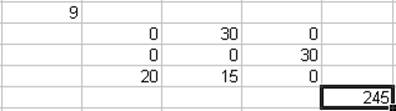
Ввод значения 30, и нажатие ОК, возвращают результаты поиска оптимального плана, подтвержденного соответствующим сообщением (опускается):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.