6. Графический метод решения матричной игры
Применяется к играм ![]() и
и
![]() .
.
Тестирование на платежной матрице:

Рис. 3.35
Возвращаемая диаграмма:
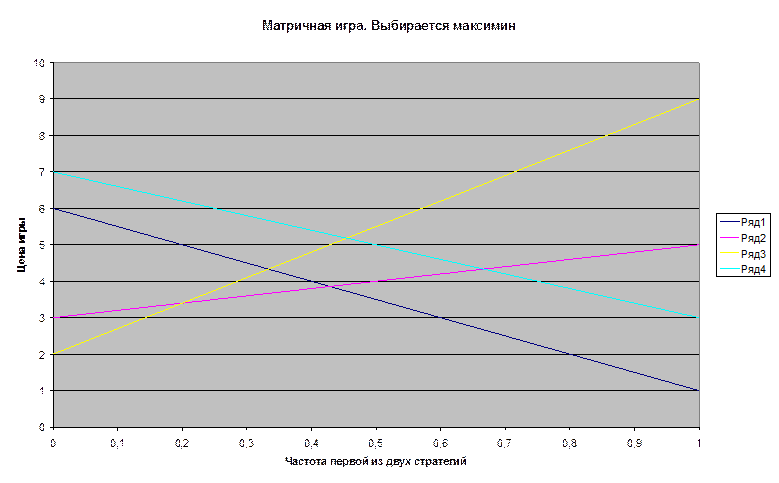
Рис. 3.36
Установка указателя мыши в точке пересечения прямых 1 и 2 дает:
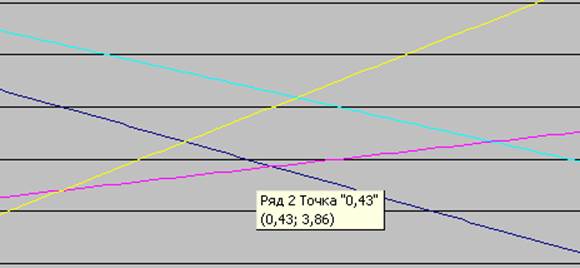
Рис. 3.37
Цена игры 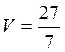 , оптимальные
частоты
, оптимальные
частоты 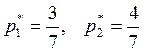 .
.
7. Критический путь – путь из начальной вершины ориентированной двухполюсной сети в конечную вершину, имеющий наибольшую длину
Пусть вершины сети ![]() , вершина
, вершина ![]() – начальная,
вершина
– начальная,
вершина ![]() – конечная. Тогда
ей соответствует
– конечная. Тогда
ей соответствует ![]() матрица
расстояний
матрица
расстояний ![]() :
:
|
Начальные \ Конечные |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
Для недостижимых за один шаг вершин ![]() .
.
Тестирование наориентированной двухполюсной сети:
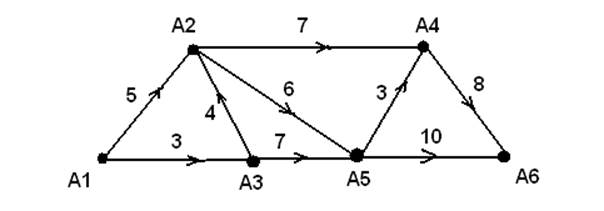
По запросу пользовательской формы вводится матрица расстояний и выделяется:
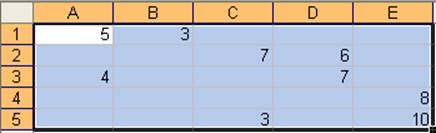
Нажатие кнопки Пуск дает:
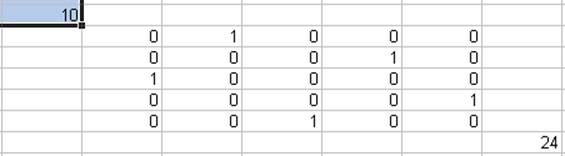
Критический путь ![]() , длина пути 24.
, длина пути 24.
8. Максимальная пропускная способность сети
Макрос DemoPotok находит максимальную пропускную способность ориентированной
двухполюсной сети ![]() . Вершина
. Вершина
![]() – начальная,
вершина
– начальная,
вершина ![]() – конечная. Сети
соответствует
– конечная. Сети
соответствует![]() матрица
матрица ![]() пропускных
способностей дуг сети, составляемая по аналогии с матрицей расстояний
предыдущего пункта.
пропускных
способностей дуг сети, составляемая по аналогии с матрицей расстояний
предыдущего пункта.
Тестирование на сети предыдущего пункта дает:
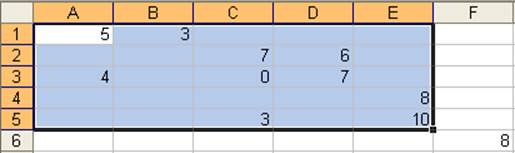
Рис. 3.43
9. Схема «гибели и размножения»
Для нее финальные вероятности вычисляются по формулам:
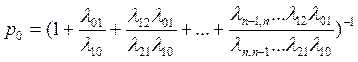 , (19)
, (19)
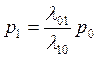
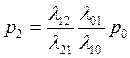 (20)
(20)
………………..
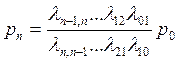 .
.
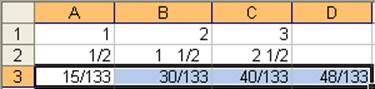
Тестирование:

Результаты:
10. Задача Эрланга
Одна из первых задач теории массового
обслуживания. Имеется n каналов (линий связи), на которые случайным образом
поступает поток заявок с интенсивностью ![]() , обслуживаемых с
интенсивностью
, обслуживаемых с
интенсивностью 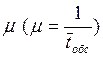 ,
, 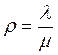 . Если все каналы
заняты, заявка систему покидает.
. Если все каналы
заняты, заявка систему покидает.
Характеристики эффективности системы:
Вероятность отказа равна вероятности того, что все каналы заняты, то есть
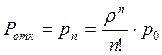 ;
;
Относительная пропускная способность – вероятность, что заявка будет обслужена, находится как вероятность противоположного события:
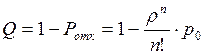 ;
;
Абсолютная пропускная способность
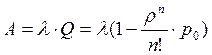 , а среднее
число занятых каналов
, а среднее
число занятых каналов
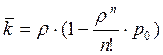 .
.
Тестирование на значениях ![]() дает:
дает:

11. Одноканальная СМО с ограниченной очередью
Состояния системы
![]() - канал свободен,
- канал свободен,
![]() -
канал занят, очереди нет,
-
канал занят, очереди нет,
![]() -
канал занят, в очереди 1 заявка,
-
канал занят, в очереди 1 заявка,
………………………………………..
![]() - канал
занят, в очереди m заявок.
- канал
занят, в очереди m заявок.
Финальные вероятности:
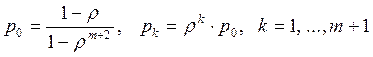 .
.
Характеристики эффективности системы:
![]() ,
,
среднее число занятых каналов
![]() ,
,
среднее число заявок в очереди
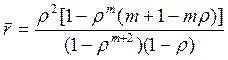 ,
,
среднее число заявок в СМО
![]() ,
,
среднее время пребывания заявки
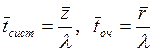 .
.
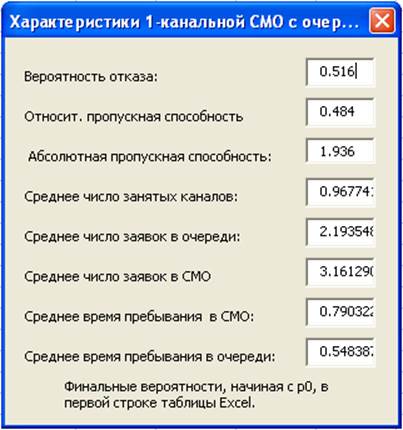
Тестирование на значениях ![]() дает:
дает:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.